Question

【题目】如图，△ABC内接于⊙O，AD与BC是⊙O的直径，延长线段AC至点G，使AG＝AD，连接DG交⊙O于点E，EF∥AB交AG于点F．

（1）求证：EF与⊙O相切．

（2）若EF＝2，AC＝4，求扇形OAC的面积．

Answer 1

【答案】（1）见解析；（2）S扇形OAC＝.

【解析】

（1）连接OE，由条件知∠D＝∠OED，证出∠OED＝∠G，可得OE∥AG，证明∠OEF＝180°∠AFE＝90°，即OE⊥EF，则EF与⊙O相切．
（2）连接OE，过点O作OH⊥AC于点H，求出CH，OH的长，再求出OC的长，得出△AOC是等边三角形，则∠AOC＝60°，可求出扇形OAC的面积．

（1）证明：如图1，连接OE，

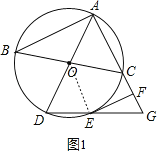
∵OD＝OE，

∴∠D＝∠OED，

∵AD＝AG，

∴∠D＝∠G，

∴∠OED＝∠G，

∴OE∥AG，

∵BC是⊙O的直径，

∴∠BAC＝90°，

∵EF∥AB，

∴∠BAF+∠AFE＝180°，

∴∠AFE＝90°，

∵OE∥AG，

∴∠OEF＝180°﹣∠AFE＝90°，

∴OE⊥EF，

∴EF与⊙O相切；

（2）解：如图2，连接OE，过点O作OH⊥AC于点H，

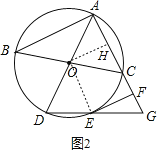
∵AC＝4，

∴CH＝，

∵∠OHF＝∠HFE＝∠OEF＝90°，

∴四边形OEFH是矩形，

∴，

在Rt△OHC中，

OC＝＝＝4，

∵OA＝AC＝OC＝4，

∴△AOC是等边三角形，

∴∠AOC＝60°，

∴S扇形OAC＝＝．