题目内容
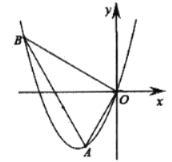
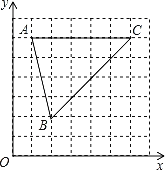
【题目】如图,坐标平面内,将△ABC放在每个小正方形的边长为l的网格中,点A(l,6),B(2,2),C(6,6),均为格点.
(1)①在B的下方找一格点D,使得∠ABC=∠CBD,画出图形,直接写出D的坐标 .
②P、Q为两格点,连PQ交BC于M,使得CM:BM=1:2,画出图形,并标出M的位置.
(2)E为一格点,作直线CE交y轴于N,若CE⊥AB,请用连线的方式找到N点,写出E的坐标 ,并画出图形.
【答案】(1)①图详见解析,(6,1);②详见解析;(2)图详见解析,(2,5).
【解析】
(1)利用轴对称可找到点D;
(2)利用△CQM∽△BPM即可找到M点;
(3)利用三角形的高线交于一点,即可找到E;
解:(1)可以将△ABC沿BC翻折,此时即有:∠ABC=∠CBD,如下图所示,
易知:D(6,1).

故答案为:D点坐标(6,1);
(2)如下图所示,在AC上取点Q,过B点作BP∥AC,在BP上取点P,
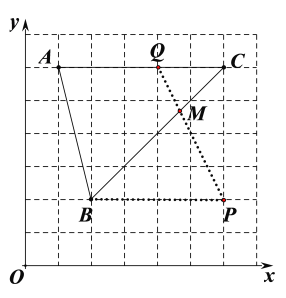
∵AC∥BP,
∴∠ACB=∠CBP,且∠CQP=∠QPB
∴△CQM∽△BPM
∴CM:BM=CQ:BP=1:2
故答案为:如上图,QP与BC的交点即为M点.
(3)如下图所示:
由(1)知,AD是△ABC的边BC的高所在的直线,BK是△ABC的边AC上的高,根据三角形的高所在的直线交于一点,故AD与BK的交点即为E点,此时连接CE并延长交y轴于N点,必有CN⊥AB,故E点的坐标为(2,5).
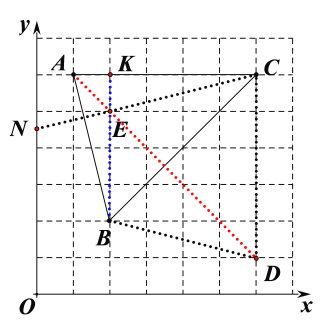
故答案为:E点的坐标为(2,5);

练习册系列答案
相关题目