题目内容
【题目】（材料阅读）
我们曾解决过课本中的这样一道题目：
如图1，四边形ABCD是正方形，E为BC边上一点，延长BA至F，使AF＝CE，连接DE，DF．……
提炼1：△ECD绕点D顺时针旋转90°得到△FAD；
提炼2：△ECD≌△FAD；
提炼3：旋转、平移、轴对称是图形全等变换的三种方式．
（问题解决）
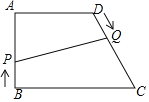
（1）如图2，四边形ABCD是正方形，E为BC边上一点，连接DE，将△CDE沿DE折叠，点C落在G处，EG交AB于点F，连接DF．
可得：∠EDF＝ °；AF，FE，EC三者间的数量关系是 ．
（2）如图3，四边形ABCD的面积为8，AB＝AD，∠DAB＝∠BCD＝90°，连接AC．求AC的长度．
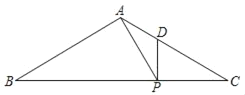
（3）如图4，在△ABC中，∠ACB＝90°，CA＝CB，点D，E在边AB上，∠DCE＝45°．写出AD，DE，EB间的数量关系，并证明．
【答案】（1）45°，AF+EC＝FE；（2）AC＝4；（3）AD2+BE2＝DE2，证明详见解析
【解析】
（1）由折叠的性质可得△CDE≌△GDE，可得CD＝DG，∠CDE＝∠GDE，∠DCE＝∠DGE＝90
，证明Rt△DAF≌Rt△DGF，可得∠ADF＝∠GDF，AF＝FG．则结论得出；
（2）延长CD到E，使DE＝BC，连接AE．证明△ADE≌△ABC，可得AE＝AC，∠EAD＝∠CAB．则答案可求出；
（3）将△ACD绕点C逆时针旋转90得到△BCH，连接EH．证明△CEH≌△CED．可得EH＝ED．可求得∠EBH＝90．可得出HB2＋BE2＝EH2．则结论得出．
（1）由折叠的性质可得△CDE≌△GDE，
∴CD＝DG，∠CDE＝∠GDE，∠DCE＝∠DGE＝90，
在Rt△DAF和Rt△DGF中，
，
∴Rt△DAF≌Rt△DGF（HL），
∴∠ADF＝∠GDF，AF＝FG．
∴∠EDF＝∠EDG+∠FDG＝
＝45，
EF＝FG+EG＝AF+EC；
故答案为：45，AF+EC＝FE．
（2）如图，延长CD到E，使DE＝BC，连接AE．
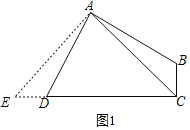
∵AB＝AD，∠DAB＝∠BCD＝90，
∴△ADE≌△ABC（SAS），
∴AE＝AC，∠EAD＝∠CAB．
∴∠EAC＝90．
∵四边形ABCD的面积为8，可得△ACE的面积为8．
∴
．
解得，AC＝4(-4舍去)．
（3）AD2+BE2＝DE2．证明如下：
如图2：将△ACD绕点C逆时针旋转90得到△BCH，连接EH．
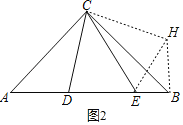
∴DC＝HC，∠DCE＝∠ECH＝45，∠CAD＝∠CBH＝45，
∵CE＝CE，
∴△CEH≌△CED（SAS）．
∴EH＝ED．
∴∠ABC+∠CBH＝∠EBH＝90．
∴HB2+BE2＝EH2．
∵AD＝BH，
∴AD2+BE2＝DE2．
