Question

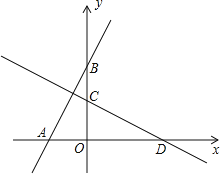
【题目】如图，在平面直角坐标系xOy中，过点A（﹣2，0）的直线交y轴正半轴于点B（0,4），将直线AB绕着点O顺时针旋转90°后，分别与x轴、y轴交于点D、C．且点C（0,3）.

（1）求直线AB的函数关系式；

（2）连接BD，求△ABD的面积.

Answer 1

【答案】（1）y=2x+4；（2）16.

【解析】试题分析：（1）利用待定系数法即可求；

（2）先求出D点坐标，然后再由A、B两点坐标即可求.

试题解析：（1）∵B（0，4），A（-2，0），

设直线解析式为y=kx+b,

则，解得，

∴直线AB的解析式为y=2x+4；

（2）∵直线CD是直线AB绕着点O顺时针旋转90°所得，

∴直线CD的解析式为，

∵点C（0,3），∴b=3,

∴直线CD的解析式为,

令y=0得x=6,∴点D（6,0），

∴.