题目内容
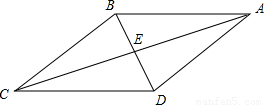
已知:如图,四边形ABCD是周长为52cm的菱形,其中对角线BD长10cm.求:(1)对角线AC的长度;
(2)菱形ABCD的面积.
【答案】分析:菱形对角线互相垂直平分,故△ABE为直角三角形,根据菱形周长可以计算AB的值,(1)在Rt△ABE中,已知AB,BE根据勾股定理可以计算AE的长,根据AE即可计算AC的长,(2)根据菱形的对角线的长度即可计算菱形ABCD的面积.
解答:解:(1)菱形对角线互相垂直平分,
故△ABE为直角三角形,
菱形ABCD的周长为52cm,
则AB=13cm,
∵BD=10cm,
∴BE=5cm,
在Rt△ABE中,AB=13cm,BE=5cm,
∴AE=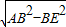 =12cm,
=12cm,
∴AC=2AE=24cm;
(2)菱形的对角线长为BD=10cm,AC=24cm,
∴菱形ABCD的面积S= BD•AC=
BD•AC= ×10cm×24cm=120cm2,
×10cm×24cm=120cm2,
答:对角线AC的长度为24cm,菱形ABCD的面积为120cm2.
点评:本题考查了勾股定理在直角三角形中的运用,考查了菱形对角线互相平分的性质,本题中正确计算AE的长是解题的关键.
解答:解:(1)菱形对角线互相垂直平分,
故△ABE为直角三角形,
菱形ABCD的周长为52cm,
则AB=13cm,
∵BD=10cm,
∴BE=5cm,
在Rt△ABE中,AB=13cm,BE=5cm,
∴AE=
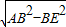 =12cm,
=12cm,∴AC=2AE=24cm;
(2)菱形的对角线长为BD=10cm,AC=24cm,
∴菱形ABCD的面积S=
 BD•AC=
BD•AC= ×10cm×24cm=120cm2,
×10cm×24cm=120cm2,答:对角线AC的长度为24cm,菱形ABCD的面积为120cm2.
点评:本题考查了勾股定理在直角三角形中的运用,考查了菱形对角线互相平分的性质,本题中正确计算AE的长是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17.
已知,如图,四边形ABCD中∠B=90°,AB=9,BC=12,AD=8,CD=17. 已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC,
已知:如图,四边形ABCD内接于⊙O,且AB∥CD,AD∥BC, 已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF
已知,如图,四边形ABCD是正方形,E、F分别是AB和AD延长线上的点,且BE=DF 已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少?
已知:如图,四边形ABCD中,BC=CD=10,AB=15,AB⊥BC,CD⊥BC,若把四边形ABCD绕直线AB旋转一周,则所得几何体的表面积是多少? 已知:如图,四边形ABCD及一点P.
已知:如图,四边形ABCD及一点P.