题目内容
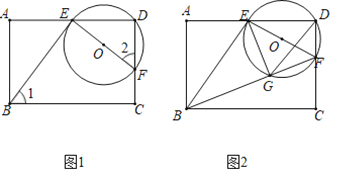
【题目】如图1,抛物线![]() 经过原点
经过原点![]() ,
,![]() 两点.
两点.
(1)求![]() 的值;
的值;
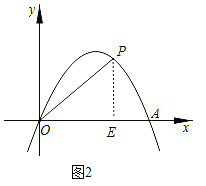
(2)如图2,点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,连接
上一点,连接![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
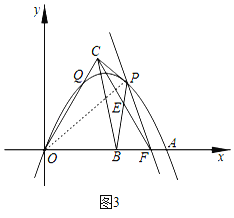
(3)如图3,在(2)的条件下,过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,作
,作![]() ,连接
,连接![]() 交抛物线于点
交抛物线于点![]() ,点
,点![]() 在线段
在线段![]() 上,连接
上,连接![]() 、
、![]() 、
、![]() ,
,![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.

【答案】(1)![]() ;(2)点
;(2)点![]() ,
,![]() ;(3)点
;(3)点![]() ,
,![]() .
.
【解析】
(1)根据待定系数法,即可得到答案;
(2)过点![]() 作
作![]() 于点
于点![]() ,设点
,设点![]() ,
,![]() ,结合
,结合![]() ,列出关于m的方程,即可求解;
,列出关于m的方程,即可求解;
(3)连接![]() ,易得直线解析式为:
,易得直线解析式为:![]() ,点
,点![]() ,
,![]() ,根据三角形内角和定理与外角的性质,得点
,根据三角形内角和定理与外角的性质,得点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 四点共圆,从而得
四点共圆,从而得![]() ,进而得点
,进而得点![]() ,过点
,过点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 四点的圆的圆心
四点的圆的圆心![]() ,
,![]() ,设点
,设点![]() ,根据两点间的距离公式,列出关于a,b的方程,得
,根据两点间的距离公式,列出关于a,b的方程,得![]() ,可得直线
,可得直线![]() 解析式为:
解析式为:![]() ,进而即可得到点Q的坐标.
,进而即可得到点Q的坐标.
(1)![]() 抛物线
抛物线![]() 经过原点
经过原点![]() ,
,![]() 两点.
两点.
![]() ,
,![]()
![]() ;
;
(2)如图2,过点![]() 作
作![]() 于点
于点![]() ,
,
![]() ,
,![]() ,
,
![]() 抛物线解析式为:
抛物线解析式为:![]()
![]() 点
点![]() 是第一象限内抛物线
是第一象限内抛物线![]() 上一点,
上一点,
![]() 设点
设点![]() ,
,![]()
![]() ,
,
![]()
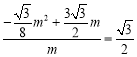 ,
,
![]() ,
,
![]() 点
点![]() ,
,![]() ;
;
(3)连接![]() ,
,
![]() 直线
直线![]() 过点
过点![]() ,
,![]() ,
,
![]() ,
,
![]() 直线解析式为:
直线解析式为:![]() ,
,
当![]() ,
,![]() ,
,
![]() 点
点![]() ,
,![]() ,
,
![]() ,且
,且![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 四点共圆,
四点共圆,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设点![]()
![]() ,
,
![]()
![]()
![]() 点
点![]()
设过点![]() ,点
,点![]() ,点
,点![]() ,点
,点![]() 四点的圆的圆心
四点的圆的圆心![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
设点![]() ,
,
![]() ,
,![]() ,
,
![]() ①,
①,![]() ②,
②,
![]() 由①②组成方程组可求:
由①②组成方程组可求:![]() ,
,
设直线![]() 解析式为:
解析式为:![]() ,且过点
,且过点![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 解析式为:
解析式为:![]() ,
,
![]()
![]() ,
,
![]() (不合题意舍去),
(不合题意舍去),![]() ,
,
![]() 点
点![]() ,
,![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目