题目内容
【题目】如图,在平行四边形ABCD中,E、F分别是AD、BC的中点,连接AF、BE交于点G,连接CE、DF交于点H.
(1)求证:四边形EGFH为平行四边形;
(2)当AB与BC满足什么条件时,四边形EGFH为矩形?并说明理由.
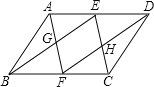
【答案】(1)证明见解析;(2)当BC=2AB时,平行四边形EGFH是矩形.理由见解析.
【解析】
(1)可分别证明四边形AFCE是平行四边形,四边形BFDE是平行四边形,从而得出GF∥EH,GE∥FH,即可证明四边形EGFH是平行四边形;
(2)证出四边形ABFE是菱形,得出AF⊥BE,即∠EGF=90°,即可得出结论.
(1)连接EF,如图所示:
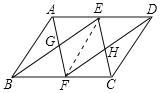
∵四边形ABCD是平行四边形,
∴AD//BC,AD=BC.
∵点E、F分别是AD、BC的中点,
∴AE=ED![]() AD,BF=FC
AD,BF=FC![]() BC,
BC,
∴AE//FC,AE=FC,
∴四边形AECF是平行四边形,
∴GF//EH.
同理可证:ED//BF且ED=BF,
∴四边形BFDE是平行四边形,
∴GE//FH,
∴四边形EGFH是平行四边形.
(2)当BC=2AB时,平行四边形EGFH是矩形.理由如下:
由(1)同理可证四边形ABFE是平行四边形,
当BC=2AB时,AB=BF,
∴四边形ABFE是菱形,
∴AF⊥BE,即∠EGF=90°,
∴平行四边形EGFH是矩形.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目