Question

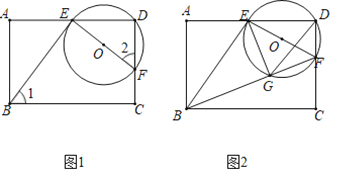
【题目】如图1，在矩形ABCD中，点E以lcm/s的速度从点A向点D运动，运动时间为t（s），连结BE，过点E作EF⊥BE，交CD于F，以EF为直径作⊙O．

（1）求证：∠1=∠2；

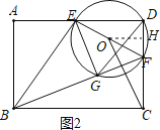
（2）如图2，连结BF，交⊙O于点G，并连结EG．已知AB=4，AD=6．

①用含t的代数式表示DF的长

②连结DG，若△EGD是以EG为腰的等腰三角形，求t的值；

（3）连结OC，当tan∠BFC=3时，恰有OC∥EG，请直接写出tan∠ABE的值．

Answer 1

【答案】（1）见解析；（2）①DF=，②t的值为3或2；（3）tan∠ABE=1

【解析】

（1）根据矩形的性质得到，，根据余角的性质即可得到结论；

（2）①根据相似三角形的性质即可得到结论；

②当时，根据相似三角形的性质得到结论；当时，根据全等三角形的性质和勾股定理即可得到结论；

（3）如图2，过作于，设，，得到，根据三角形的中位线的性质得到，根据三角函数的定义得到，，根据相似三角形的性质即可得到结论．

（1）∵四边形是矩形

∴，

∴

∵

∴

∵

∴

∴

（2）①∵，

∴

∴

∵，，

∴

∴

②当时

∴

∵，

∴

∵

∴

∴

∴

∴

∴

当时，∴

∵，

∴

∵，

∴

∴

∵

∴

∴

综上所述，若是以为腰的等腰三角形，的值为或．

（3）

理由：如图2，过作于

∵

设，

∵

∴

∵，

∴

∵

∴

∵，

∴

∴

∴，

∴，

由，得:

即

解得：，

∴