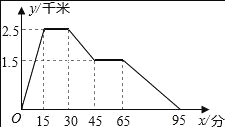
题目内容
【题目】如图所示,矩形ABCD中,AB=6,BD=10.Rt△EFG的直角边GE在CB的延长线上,E点与矩形的B点重合,∠FGE=90°,已知GE+AB=BC,FG=2GE.将矩形ABCD固定,把Rt△EFG沿着射线BC方向按每秒1个单位运动,直到点G到达点C停止运动.设Rt△EFG的运动时间为t秒(t>0).
(1)求出线段FG的长,并求出当点F恰好经过BD时,运动时间t的值;
(2)在整个运动过程中,设Rt△EFG与△BCD的重合部分面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围.

【答案】(1)FG=4,t=![]() ;(2)S=
;(2)S=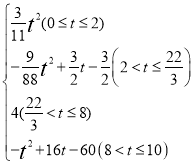 .
.
【解析】
试题分析:(1)利用矩形的性质和勾股定理易得FG,利用相似三角形的性质可得BG的长,进而可求出t的值;(2)①如图1,当0<t≤2时,根据三角形的面积公式求得结论;②如图2,当2<t≤![]() 时,根据三角形的面积公式即可得到结论;③如图3,当
时,根据三角形的面积公式即可得到结论;③如图3,当![]() <t≤8时,S=4④当8<t≤10时根据两三角形的面积差即可得到结论.
<t≤8时,S=4④当8<t≤10时根据两三角形的面积差即可得到结论.
试题解析:(1)在矩形ABCD中,AB=6,BD=10,∴由勾股定理得:BC=8,∵在Rt△EFG中,GE+AB=BC,FG=2GE.∴FG=4 ,当点F恰好经过BD时,∵∠FGE=90°,∠C=90°,∴FG∥DC,∴△BFG∽△BCD,∴![]() ,∴BG=
,∴BG=![]() ,∴BE=
,∴BE=![]() ,∴当点F恰好经过BD时,t=
,∴当点F恰好经过BD时,t=![]() .(2)①当0≤t≤2时,如图1,∵MN∥CD,∴三角形BMN相似三角形BCD,三角形MNE相似三角形FGE,设MN=x,则BN=
.(2)①当0≤t≤2时,如图1,∵MN∥CD,∴三角形BMN相似三角形BCD,三角形MNE相似三角形FGE,设MN=x,则BN=![]() ,NE=0.5x,则BE=
,NE=0.5x,则BE=![]() x=t,∴MN=
x=t,∴MN=![]() ,S=
,S=![]() t2,
t2,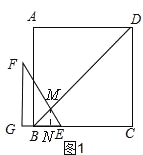 ②当2<t≤
②当2<t≤![]() 时,如图2,S=﹣
时,如图2,S=﹣![]() t2+
t2+![]() t﹣
t﹣![]() ,
,
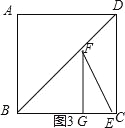
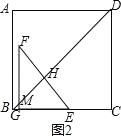 ③当
③当![]() <t≤8时,如图3,S=4,
<t≤8时,如图3,S=4,
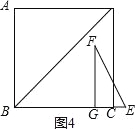
 ④当8<t≤10时,如图4,S=﹣t2+16t﹣60,
④当8<t≤10时,如图4,S=﹣t2+16t﹣60,
 ,综上可知S与t之间的函数关系式为:S=
,综上可知S与t之间的函数关系式为:S=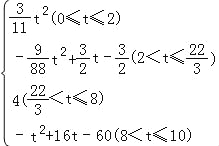 .
.