题目内容
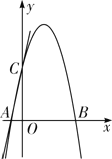
【题目】如图，直线y＝5x＋5交x轴于点A，交y轴于点C，过A，C两点的二次函数y＝ax2＋4x＋c的图象交x轴于另一点B.
(1)求二次函数的表达式；
(2)连接BC，点N是线段BC上的动点，作ND⊥x轴交二次函数的图象于点D，求线段ND长度的最大值；
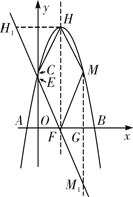
(3)若点H为二次函数y＝ax2＋4x＋c图象的顶点，点M(4，m)是该二次函数图象上一点，在x轴，y轴上分别找点F，E，使四边形HEFM的周长最小，求出点F、E的坐标．
【答案】(1) y＝－x2＋4x＋5；(2)
;(3) F (
，0)，E(0，
)．
【解析】
（1）先根据坐标轴上点的坐标特征由一次函数的表达式求出A，C两点的坐标，再根据待定系数法可求二次函数的表达式；
（2）根据坐标轴上点的坐标特征由二次函数的表达式求出B点的坐标，根据待定系数法可求一次函数BC的表达式，设ND的长为d，N点的横坐标为n，则N点的纵坐标为-n+5，D点的坐标为D（n，-n2+4n+5），根据两点间的距离公式和二次函数的最值计算可求线段ND长度的最大值；
（3）由题意可得二次函数的顶点坐标为H（2，9），点M的坐标为M（4，5），作点H（2，9）关于y轴的对称点H1，可得点H1的坐标，作点M（4，5）关于x轴的对称点HM1，可得点M1的坐标连结H1M1分别交x轴于点F，y轴于点E，可得H1M1+HM的长度是四边形HEFM的最小周长，再根据待定系数法可求直线H1M1解析式，根据坐标轴上点的坐标特征可求点F、E的坐标．
解：(1)∵直线y＝5x＋5交x轴于点A，交y轴于点C，
∴A(－1，0)，C(0，5)，
∵二次函数y＝ax2＋4x＋c的图象过A，C两点，
∴
，
解得
，
∴二次函数的表达式为y＝－x2＋4x＋5；
(2)如解图①，
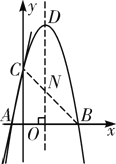
第2题解图①
∵点B是二次函数的图象与x轴的交点，
∴由二次函数的表达式为y＝－x2＋4x＋5得，点B的坐标B(5，0)，
设直线BC解析式为y＝kx＋b，
∵直线BC过点B(5，0)，C(0，5)，
∴
，
解得
，
∴直线BC解析式为y＝－x＋5，
设ND的长为d，N点的横坐标为n，
则N点的坐标为(n，－n＋5)，
D点的坐标为(n，－n2＋4n＋5)，
则d＝|－n2＋4n＋5－(－n＋5)|，
由题意可知：－n2＋4n＋5＞－n＋5，
∴d＝－n2＋4n＋5－(－n＋5)＝－n2＋5n＝－(n－
)2＋，
∴当n＝时，线段ND长度的最大值是；
（3）∵点M(4，m)在抛物线y＝－x2＋4x＋5上，
∴m＝5，∴M(4，5)．
∵抛物线y＝－x2＋4x＋5＝－(x－2)2＋9，
∴顶点坐标为H(2，9)，
如解图②，作点H(2，9)关于y轴的对称点H1，则点H1的坐标为H1(－2，9)；作点M(4，5)关于x轴的对称点M1，则点M1的坐标为M1(4，－5)，连接H1M1分别交x轴于点F，y轴于点E，∴H1M1＋HM的长度是四边形HEFM的最小周长，则点F，E即为所求的点．
设直线H1M1的函数表达式为y＝mx＋n，
∵直线H1M1过点H1(－2，9)，M1(4，－5)，
∴
，
解得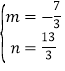
，
∴y＝－
x＋，
∴当x＝0时，y＝，即点E坐标为(0，)，
当y＝0时，x＝，即点F坐标为(，0)，
故所求点F，E的坐标分别为(，0)，(0，)．
