题目内容
已知:如图,梯形ABCD中,AD∥BC,∠B=90°,AD=AB=4,BC=7,点E在BC边上,将△CDE沿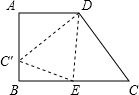 DE折叠,点C恰好落在AB边上的点C'处.
DE折叠,点C恰好落在AB边上的点C'处.(1)求∠C'DE的度数;
(2)求△C'DE的面积.
分析:(1)首先作DF⊥BC于F,根据已知证出△AC′D≌△FCD,再求出∠C′DE=∠CDE,即可得出答案;
(2)根据EC=x,则BE=7-x,C′E=x,再根据勾股定理求出EC的长,即可求出△C′DE的面积.
(2)根据EC=x,则BE=7-x,C′E=x,再根据勾股定理求出EC的长,即可求出△C′DE的面积.
解答: 解:(1)过点D作DF⊥BC于F.
解:(1)过点D作DF⊥BC于F.
∵AD∥BC,∠B=90°,AD=AB,
∴四边形ABFD是正方形.
∴DF=BF=AB=4,FC=3,
在Rt△DFC中,CD=
=
=5,
∴C′D=5,
∵AD=FD,∠A=∠DFC=90°,C′D=CD,
∴△AC′D≌△FCD,
∴∠ADC′=∠FDC,AC′=FC=3,
∴∠ADF=∠ADC′+∠C′DF=∠FDC+∠C′DF=∠C′DC=90°,
∵∠C′DE=∠CDE,
∴∠C′DE=45°;
(2)设EC=x,则BE=7-x,C′E=x,
∵AC′=3,
∴BC'=1,
在Rt△BEC′中(7-x)2+1=x2
解方程,得:x=
,
∴S△C′DE=S△CDE=
EC•DF=
×
×4=
=7
.
 解:(1)过点D作DF⊥BC于F.
解:(1)过点D作DF⊥BC于F.∵AD∥BC,∠B=90°,AD=AB,
∴四边形ABFD是正方形.
∴DF=BF=AB=4,FC=3,
在Rt△DFC中,CD=
| DF2+FC2 |
| 42+32 |
∴C′D=5,
∵AD=FD,∠A=∠DFC=90°,C′D=CD,
∴△AC′D≌△FCD,
∴∠ADC′=∠FDC,AC′=FC=3,
∴∠ADF=∠ADC′+∠C′DF=∠FDC+∠C′DF=∠C′DC=90°,
∵∠C′DE=∠CDE,
∴∠C′DE=45°;
(2)设EC=x,则BE=7-x,C′E=x,
∵AC′=3,
∴BC'=1,
在Rt△BEC′中(7-x)2+1=x2
解方程,得:x=
| 25 |
| 7 |
∴S△C′DE=S△CDE=
| 1 |
| 2 |
| 1 |
| 2 |
| 25 |
| 7 |
| 50 |
| 7 |
| 1 |
| 7 |
点评:此题主要考查了翻折变换和全等三角形的判定以及勾股定理的应用等知识,得出△AC′D≌△FCD和利用勾股定理求出EC的长是解决问题的关键.

练习册系列答案
相关题目
 9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( )
9、已知:如图,梯形ABCD中,AD∥BC,AB=CD,对角线AC与BD相交于点O,则图中全等三角形共有( ) 已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC=
已知:如图,梯形ABCD中,AD∥BC,∠DAB=120°,tanC= 8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB=
8、已知,如图,梯形ABCD中,AB∥CD,△COD与△AOB的周长比为1:2,则CD:AB= 已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.
已知:如图,梯形ABCD中,AB∥CD,AD=BC,对角线AC、BD交于M,AB=2,CD=4,∠CMD=90°,求:BD的长.