题目内容
【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为50和39,则△EDF的面积为( ) 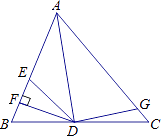
A.11
B.5.5
C.7
D.3.5
【答案】B
【解析】解:作DM=DE交AC于M,作DN⊥AC于点N, ∵DE=DG,
∴DM=DG,
∵AD是△ABC的角平分线,DF⊥AB,
∴DF=DN,
在Rt△DEF和Rt△DMN中,![]() ,
,
∴Rt△DEF≌Rt△DMN(HL),
∵△ADG和△AED的面积分别为50和39,
∴S△MDG=S△ADG﹣S△ADM=50﹣39=11,
S△DNM=S△EDF= ![]() S△MDG=
S△MDG= ![]() ×11=5.5.
×11=5.5.
故选B.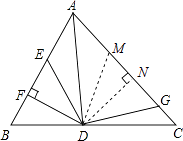
作DM=DE交AC于M,作DN⊥AC,利用角平分线的性质得到DN=DF,将三角形EDF的面积转化为三角形DNM的面积来求.

练习册系列答案
相关题目