题目内容
【题目】如图①，BC是⊙O的直径，点A在⊙O上，AD⊥BC垂足为D，弧AE＝弧AB，BE分别交AD、AC于点F、G．
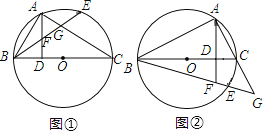
（1）判断△FAG的形状，并说明理由；
（2）如图②若点E与点A在直径BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变（1）中的结论还成立吗？请说明理由．
（3）在（2）的条件下，若BG＝26，DF＝5，求⊙O的直径BC．
【答案】（1）△FAG是等腰三角形，理由见解析；（2）成立，理由见解析；（3）BC＝
．
【解析】
（1）首先根据圆周角定理及垂直的定义得到∠BAD+∠CAD＝90°，∠C+∠CAD＝90°，从而得到∠BAD＝∠C，然后利用等弧对等角等知识得到AF＝BF，从而证得FA＝FG，判定等腰三角形；
（2）成立，同（1）的证明方法即可得答案；
（3）由（2）知∠DAC＝∠AGB，推出∠BAD＝∠ABG，得到F为BG的中点根据直角三角形的性质得到AF＝BF＝
BG＝13，求得AD＝AF﹣DF＝13﹣5＝8，根据勾股定理得到BD＝12，AB＝4
，由∠ABC＝∠ABD，∠BAC＝∠ADB＝90°可证明△ABC∽△DBA，根据相似三角形的性质即可得到结论．
（1）△FAG等腰三角形；理由如下：
∵BC为直径，
∴∠BAC＝90°，
∴∠ABE+∠AGB＝90°，
∵AD⊥BC，
∴∠ADC＝90°，
∴∠ACD+∠DAC＝90°，
∵
，
∴∠ABE＝∠ACD，
∴∠DAC＝∠AGB，
∴FA＝FG，
∴△FAG是等腰三角形．
（2）成立，理由如下：
∵BC为直径，
∴∠BAC＝90°，
∴∠ABE+∠AGB＝90°，
∵AD⊥BC，
∴∠ADC＝90°，
∴∠ACD+∠DAC＝90°，
∵，
∴∠ABE＝∠ACD，
∴∠DAC＝∠AGB，
∴FA＝FG，
∴△FAG是等腰三角形．
（3）由（2）知∠DAC＝∠AGB，且∠BAD+∠DAC＝90°，∠ABG+∠AGB＝90°，
∴∠BAD＝∠ABG，
∴AF＝BF，
∵AF＝FG，
∴BF=GF，即F为BG的中点，
∵△BAG为直角三角形，
∴AF＝BF＝BG＝13，
∵DF＝5，
∴AD＝AF﹣DF＝13﹣5＝8，
∴在Rt△BDF中，BD＝
＝12，
∴在Rt△BDA中，AB＝
＝4，
∵∠ABC＝∠ABD，∠BAC＝∠ADB＝90°，
∴△ABC∽△DBA，
∴
＝
，
∴
＝
，
∴BC＝，
∴⊙O的直径BC＝．
