题目内容
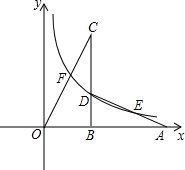 如图,在平面直角坐标系中,A为(8,0),B是线段OA上的一点,点C在第一象限,CB⊥OA于点B,且CB=5,D为CB上一点,BD=2,设OB=a,经过点D的双曲线y=
如图,在平面直角坐标系中,A为(8,0),B是线段OA上的一点,点C在第一象限,CB⊥OA于点B,且CB=5,D为CB上一点,BD=2,设OB=a,经过点D的双曲线y=| k |
| x |
考点:反比例函数综合题
专题:综合题
分析:根据A坐标,CB垂直于OA,且CB,BD,以及OB,表示出B,C,D坐标,根据E为AD中点,利用线段中点坐标公式表示出E坐标,由D、E在反比例函数图象上,将D、E坐标代入反比例解析式分别表示出k,消去k得到关于a的方程,求出方程的解得到a的值,确定出C坐标,得出反比例解析式,进而确定出直线OC解析式,两解析式联立消去y求出x的值,进而求出y的值,即为F坐标.
解答:解:∵A(8,0),CB⊥OA,CB=5,BD=2,OB=a,
∴B(a,0),C(a,5),D(a,2),
∵E为AD的中点,
∴E(
,1),
∵D、E在双曲线y=
上,
∴将D坐标代入双曲线解析式得:2=
,即k=2a,
将E坐标代入双曲线解析式得:1=
,即k=
,
∴2a=
,
解得:a=
,
∴k=2a=
,
∴C(
,5),
∴双曲线解析式为y=
①,
设直线OC解析式为y=mx,
将C坐标代入得:5=
m,即m=
,
∴直线OC解析式为y=
x②,
联立①②,消去y得:
=
x,即x2=
,
解得:x1=
,x2=-
(C在第一象限,故舍去),
∴y=
×
=
,
则F坐标为(
,
).
∴B(a,0),C(a,5),D(a,2),
∵E为AD的中点,
∴E(
| 8+a |
| 2 |
∵D、E在双曲线y=
| k |
| x |
∴将D坐标代入双曲线解析式得:2=
| k |
| a |
将E坐标代入双曲线解析式得:1=
| k | ||
|
| 8+a |
| 2 |
∴2a=
| 8+a |
| 2 |
解得:a=
| 8 |
| 3 |
∴k=2a=
| 16 |
| 3 |
∴C(
| 8 |
| 3 |
∴双曲线解析式为y=
| 16 |
| 3x |
设直线OC解析式为y=mx,
将C坐标代入得:5=
| 8 |
| 3 |
| 15 |
| 8 |
∴直线OC解析式为y=
| 15 |
| 8 |
联立①②,消去y得:
| 16 |
| 3x |
| 15 |
| 8 |
| 128 |
| 45 |
解得:x1=
8
| ||
| 15 |
8
| ||
| 15 |
∴y=
| 15 |
| 8 |
8
| ||
| 15 |
| 10 |
则F坐标为(
8
| ||
| 15 |
| 10 |
点评:此题属于反比例函数综合题,涉及的知识有:待定系数法求函数解析式,坐标与图形性质,坐标与图形性质,线段中点坐标公式,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目