题目内容
如图,AB为⊙O的直径,AB=4,点C在⊙O上,CF⊥OC,且CF=BF.
小题1:证明BF是⊙O的切线;
小题2:设AC与BF的延长线交于点M,若MC=6,求∠MCF的大小.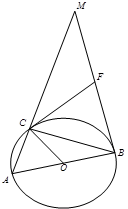
小题1:证明BF是⊙O的切线;
小题2:设AC与BF的延长线交于点M,若MC=6,求∠MCF的大小.
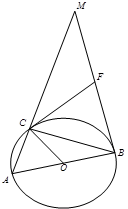
小题1:见解析。
小题2:30°
证明:连接OF.
(1) ∵ CF⊥OC,
∴ ∠FCO=90°.
∵ OC=OB,
∴ ∠BCO=∠CBO.
∵ FC=FB,
∴ ∠FCB=∠FBC.
∴ ∠BCO+∠FCB =∠CBO+∠FBC.
即 ∠FBO=∠FCO=90°.
∴ OB⊥BF.
∵ OB是⊙O的半径,
∴ BF是⊙O的切线.
(2)∵ ∠FBO=∠FCO=90°,
∴ ∠MCF+∠ACO =90°,∠M+∠A =90°.
∵ OA=OC,
∴ ∠ACO=∠A.
∴ ∠FCM=∠M.
易证△ACB∽△ABM,
∴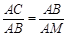 .
.
∵ AB=4,MC=6,
∴ AC=2.
∴ AM=8,BM=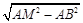 =
=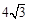 .
.
∴cos∠MC F =cosM =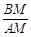 =
= .
.
∴ ∠MCF=30°.
(1) ∵ CF⊥OC,
∴ ∠FCO=90°.
∵ OC=OB,
∴ ∠BCO=∠CBO.
∵ FC=FB,
∴ ∠FCB=∠FBC.
∴ ∠BCO+∠FCB =∠CBO+∠FBC.
即 ∠FBO=∠FCO=90°.
∴ OB⊥BF.
∵ OB是⊙O的半径,
∴ BF是⊙O的切线.
(2)∵ ∠FBO=∠FCO=90°,
∴ ∠MCF+∠ACO =90°,∠M+∠A =90°.
∵ OA=OC,
∴ ∠ACO=∠A.
∴ ∠FCM=∠M.
易证△ACB∽△ABM,
∴
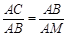 .
.∵ AB=4,MC=6,
∴ AC=2.
∴ AM=8,BM=
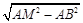 =
=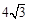 .
.∴cos∠MC F =cosM =
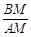 =
= .
. ∴ ∠MCF=30°.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
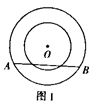
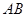 为
为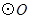 的直径,弦
的直径,弦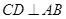 于点
于点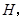 连结
连结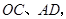 若
若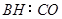
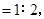
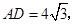 则
则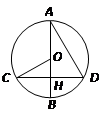
 (2)若圆的半径为1,△ABE是等边三角形,求BP的长.
(2)若圆的半径为1,△ABE是等边三角形,求BP的长.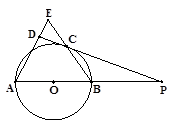
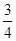
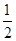
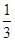
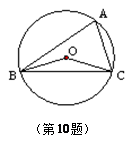
 ;
;
 来表示,则
来表示,则



