题目内容
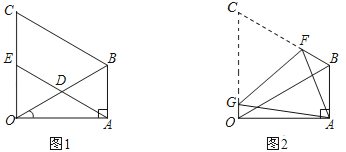
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.
(1)求证:EG=CG;EG⊥CG.
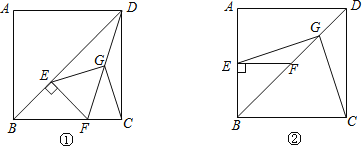
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)见解析;(2)结论仍然成立,证明见解析
【解析】
试题分析:(1)根据直角三角形斜边中线的性质以及三角形外角定理即可证明.
(2)作GM⊥BC于M,⊥AB于N交CD于H,只要证明△GNE≌△GMC即可解决问题.
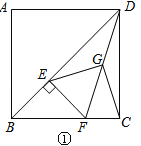
证明:(1)如图①中,∵四边形ABCD是正方形,
∴∠BCD=∠ADC=90°,∠BDC=![]() ,
,
∵EF⊥BD,
∴∠DEF=90°,
∵GF=GD,
∴EG=DG=GF=![]() DF,GC=DG=GF=
DF,GC=DG=GF=![]() DF,
DF,
∴EG=GC,∠GED=∠GDE,∠GCD=∠GDC,
∵∠EGF=∠GED+∠GDE=2∠EDG,∠CGF=∠GCD+∠GDC=2∠GDC,
∴∠EGC=∠EGF+∠CGF=2∠EDG+2∠GDC=2(∠EDG+∠GDC)=90°,
∴EG⊥GC.
(2)图②中,结论仍然成立.
理由:作GM⊥BC于M,⊥AB于N交CD于H.
∵四边形ABCD是正方形,
∴∠A=∠ADC=90°,∠ABD=∠DBC=∠BDC=45°
∴GM=GN,
∵∠A=∠ANG=∠ADH=90°,
∴四边形ANHD是矩形,
∴∠DHN=90°,∠GDH=∠HGD=45°,
∴HG=DH=AN,同理GH=CM,
∵∠ENG=∠A=∠BEF=90°,
∴EF∥GN∥AD,∵GF=GD,
∴AN=NE=GH=MC,
在△GNE和△GMC中,
 ,
,
∴△GNE≌△GMC,
∴GE=GC,∠NGE=∠MGC,
∴∠EGC=∠NGM=90°,
∴EG⊥GC.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案