Question

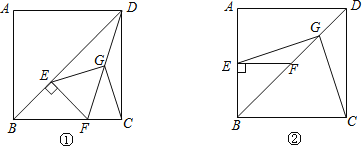
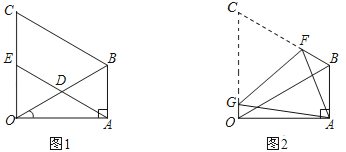
【题目】如图1，在△OAB中，∠OAB=90°，∠AOB=30°，OB=8．以OB为边，在△OAB外作等边△OBC，D是OB的中点，连接AD并延长交OC于E．

（1）求证：四边形ABCE是平行四边形；

（2）如图2，将图1中的四边形ABCO折叠，使点C与点A重合，折痕为FG，求OG的长．

Answer 1

【答案】（1）证明见解析；（2）1.

【解析】

试题分析：（1）首先根据直角三角形中斜边上的中线等于斜边的一半可得DO=DA，再根据等边对等角可得∠DAO=∠DOA=30°，进而算出∠AEO=60°，再证明BC∥AE，CO∥AB，进而证出四边形ABCE是平行四边形；

（2）设OG=x，由折叠可得：AG=GC=8-x，再利用三角函数可计算出AO，再利用勾股定理计算出OG的长即可．

试题解析：（1）∵Rt△OAB中，D为OB的中点，

∴AD=OB，OD=BD=OB

∴DO=DA，

∴∠DAO=∠DOA=30°，∠EOA=90°，

∴∠AEO=60°，

又∵△OBC为等边三角形，

∴∠BCO=∠AEO=60°，

∴BC∥AE，

∵∠BAO=∠COA=90°，

∴CO∥AB，

∴四边形ABCE是平行四边形；

（2）设OG=x，由折叠可得：AG=GC=8-x，

在Rt△ABO中，

∵∠OAB=90°，∠AOB=30°，BO=8，

∴AO=BOcos30°=8×=4，

在Rt△OAG中，OG2+OA2=AG2，

x2+（4）2=（8-x）2，

解得：x=1，

∴OG=1．