题目内容
【题目】某商场经销-种进价为每千克50元的水产品,据市场分析,每千克售价为60元时,月销售量为![]() ,销售单价每涨1元时,月销售量就减少
,销售单价每涨1元时,月销售量就减少![]() ,针对这种情况,请解答以下问题:
,针对这种情况,请解答以下问题:
(1)当销售单价定为65元时,计算销售量和月销售利润;
(2)若想在月销售成本不超过12000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
【答案】(1)销售量:450kg;月销售利润:6750元;(2)销售单价定为90元时,月销售利润达到8000元,且销售成本不超过12000元
【解析】
(1)利用每千克水产品的销售利润×月销售量=月销售利润列出函数即可;
(2)由函数值为8000,列出一元二次方程解决问题.
解:(1)销售量:![]() ,
,
月销售利润:![]() (元);
(元);
(2)因为月销售成本不超过12000元,
∴月销售数量不超过![]() ;
;
设销售定价为![]() 元,由题意得:
元,由题意得:
![]() ,
,
解得![]() ;
;
当![]() 时,
时,
月销售量为![]() ,满足题意;
,满足题意;
当![]() 时,
时,
月销售量为![]() ,不合题意,应舍去.
,不合题意,应舍去.
∴销售单价定为90元时,月销售利润达到8000元,且销售成本不超过12000元.

 一课一练课时达标系列答案
一课一练课时达标系列答案【题目】某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满,根据下表提供的信息,解答以下问题
土特产种类 | 甲 | 乙 | 丙 |
每辆汽车运载量(吨) | 8 | 6 | 5 |
每吨土特产获利(百元) | 12 | 16 | 10 |
(1)设装运甲种土特产的车辆数为x,装运乙种土特产的车辆数为y,求y与x之间的函数关系式;
(2)如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值
【题目】某校“心灵信箱”的设立,为师、生之间的沟通开设了一个书面交流的渠道.为了解九年级学生对“心灵信箱”开通两年来的使用情况,某课题组对该校九年级全体学生进行了一次问卷调查,并根据调查结果绘制了如下尚不完整的统计图.
两年来,你通过“心灵信箱”给老师总共投递过几封信? |
A.没投过 B.一封 C.两封 D.三封或以上 |
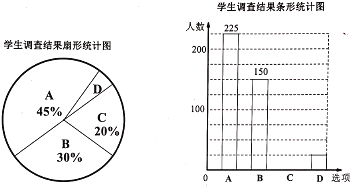
根据以上图表,解答下列问题:
(1)该校九年级学生共有____人;
(2)学生调查结果扇形统计图中,扇形![]() 的圆心角度数是______;
的圆心角度数是______;
(3)请你补全条形统计图;
(4)根据调查结果可以推断:两年来,该校九年级学生通过“心灵信箱”投递出信件总数至少有_____封.