题目内容
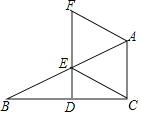
【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD= ![]() ,AE=3,求AF的长.
,AE=3,求AF的长.
【答案】
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴∠ADF=∠CED,∠B+∠C=180°;
∵∠AFE+∠AFD=180°,∠AFE=∠B,
∴∠AFD=∠C,
∴△ADF∽△DEC
(2)解:∵CD=AB=4,AE⊥BC,
∴AE⊥AD; 在Rt△ADE中,DE= ![]() ,
,
∵△ADF∽△DEC,
∴ ![]() ;
;
∴ ![]() ,
,
解得AF= ![]()
【解析】(1)根据平行四边形的性质证出AD∥BC,AB∥CD,结合已知∠AFE=∠B.得出∠ADF=∠CED,∠AFD=∠C再根据两组角对应相等的两个三角形相似证得结论。
(2)根据平行四边形的性质及已知AE⊥BC,证明△ADE是直角三角形,利用勾股定理求出DE的长,再根据相似三角形的性质(△ADF∽△DEC)。得对应线段成比例,建立方程求出AF的长。

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目