题目内容
如图，在菱形ABCD中∠ABC=60゜，E为AB中点，P为对角线BD上任意一点，AB=2，则PE+PA的最小值为______．
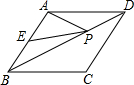
作点E′和E关于BD对称．则连接AE′交BD于点P，
∵四边形ABCD是菱形，AB=2，E为AB中点，
∴点E′是BC的中点，
∴BE′=1，
∴BE′=
AB，
∴AE′⊥BC
∴AE′=
=
=
．
故答案为
．
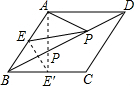
∵四边形ABCD是菱形，AB=2，E为AB中点，
∴点E′是BC的中点，
∴BE′=1，
∴BE′=
| 1 |
| 2 |
∴AE′⊥BC
∴AE′=
| AB2-BE′2 |
| 22-12 |
| 3 |
故答案为
| 3 |
练习册系列答案
名校课堂系列答案
相关题目
