题目内容
设A、B两点的坐标分别为(1,1)和(4,3),P点是x轴上的点,则PA+PB的最小值是______.
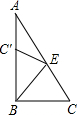
作点A关于x轴的对称点A',则A′坐标为(1,-1),
连接A′B交x轴于一点,此点就是点P,此时PA+PB最小,
作BE⊥y于一点E,延长A′A交BE于一点M,
∵PB=PA′,
∴PA+PB=BA′,
∵A、B两点的坐标分别为(1,1)和(4,3),A′坐标为(1,-1),
∴BM=4-1=3,MA′=1+3=4,
∴BA′=
=
=5.
∴PA+PB的最小值是5.
故答案为:5.

连接A′B交x轴于一点,此点就是点P,此时PA+PB最小,
作BE⊥y于一点E,延长A′A交BE于一点M,
∵PB=PA′,
∴PA+PB=BA′,
∵A、B两点的坐标分别为(1,1)和(4,3),A′坐标为(1,-1),
∴BM=4-1=3,MA′=1+3=4,
∴BA′=
| BM2+MA′2 |
| 32+42 |
∴PA+PB的最小值是5.
故答案为:5.


练习册系列答案
相关题目