Question

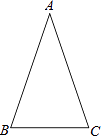
【题目】如图，在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，分别交AB、AC于点D、E．若AB=5，AC=4，则△ADE的周长是 ．

Answer 1

【答案】9
【解析】解：∵在△ABC中，∠B与∠C的平分线交于点O， ∴∠DBO=∠CBO，∠ECO=∠BCO，
∵DE∥BC，
∴∠DOB=∠CBO，∠EOC=∠BCO，
∴∠DBO=∠DOB，∠ECO=∠EOC，
∴OD=BD，OE=CE，
∵AB=5，AC=4，
∴△ADE的周长为：AD+DE+AE=AD+DO+EO+AE=AD+DB+EC+AE=AB+AC=5+4=9．
故答案为：9．
由在△ABC中，∠B与∠C的平分线交于点O，过点O作DE∥BC，易证得△DOB与△EOC是等腰三角形，即DO=DB，EO=EC，继而可得△ADE的周长等于AB+AC，即可求得答案．