题目内容
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…,如此进行下去,直至得Cn . 若P(2014,m)在第n段抛物线Cn上,则m= 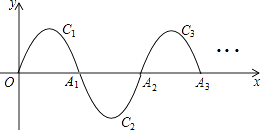
【答案】-2
【解析】解:∵一段抛物线:y=﹣x(x﹣3)(0≤x≤3),∴图象与x轴交点坐标为:(0,0),(3,0),
∵将C1绕点A1旋转180°得C2 , 交x轴于点A2;
将C2绕点A2旋转180°得C3 , 交x轴于点A3;
…
如此进行下去,直至得Cn .
∴C672的解析式与x轴的交点坐标为(2013,0),(2016,0),且图象在x轴下方,
∴C672的解析式为:y672=(x﹣2013)(x﹣2016),
当x=2014时,m=(2014﹣2013)×(2014﹣2016)=﹣2.
故答案为:﹣2.
根据图象的旋转变化规律以及二次函数的平移规律得出平移后解析式,进而求出m的值.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目






