题目内容
【题目】如图,在△ABC中,AB=AC,∠A=36°,且BC=2,则AB= . 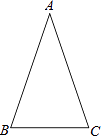
【答案】![]()
【解析】解:如图,作∠ABC的平分线交AC于D, 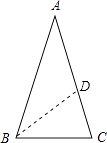
∵AB=AC,且∠A=36°,
∴∠ABC=∠C=72°,
∴∠ABD=∠CBD=36°,
∴DA=DB,
而∠BDC=∠A+∠ABD=72°,
∴BD=BC,
∴AD=BC,
∵∠CBD=∠A,∠BCD=∠ACB,
∴△BCD∽△ABC,
∴BC:AC=CD:BC,
∴BC2=CDAD,
∴AD2=CDAD,
∴点D为AC的黄金分割点,
∴ ![]() =
= ![]() ,
,
即 ![]() =
= ![]() ,
,
∴AC= ![]() =AB,
=AB,
所以答案是: ![]() .
.
【考点精析】本题主要考查了等腰三角形的性质和黄金分割的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角);把线段AB分成两条线段AC,BC(AC>BC),并且使AC是AB和BC的比例中项,叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC=0.618AB才能正确解答此题.

练习册系列答案
相关题目