Question

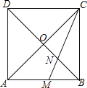
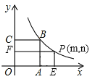
【题目】如图所示，已知正方形的面积为，点在函数的图象上，点是函数的图象上动点，过点分别作轴、轴的垂线，垂足分别为、，若设矩形和正方形不重合的两部分的面积和为．

求点坐标和的值；

写出关于的函数关系和的最大值．

Answer 1

【答案】 ；当时，取得最大值，此时最大值为．

【解析】

（1）由四边形OABC为正方形，面积为9，求出正方形的边长为3，得到AB与OA为3，由B在第一象限确定出B的坐标，将B坐标代入反比例解析式中，即可求出k的值；

（2）由P的坐标，表示PE与OE，由OEOA表示出AE的长，矩形OEPF和正方形OABC不重合的两部分为矩形，面积为PE与AE乘积，再由P在反比例函数图象上，将P坐标代入反比例解析式，用m表示出n，列出S关于m的函数关系式，由m的范围，得出反比例函数p＝为减函数，可得出S为关于m的增函数，将m的最大值9代入，即可求出S的最大值．

∵正方形的面积为，

∴正方形的边长为，即，，

∴点坐标为；

又∵点是函数的图象上的一点，

∴，

∴；

由，得到点在点的右侧，则，，

∴，

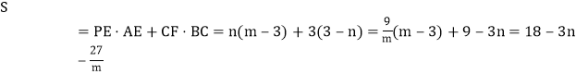当时，反比例函数为减函数，为关于的增函数，

∴当时，取得最大值，此时最大值为．