题目内容
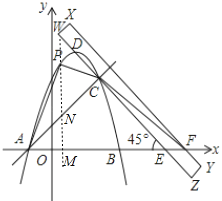
【题目】如图,已知抛物线y=ax2+2x+6(a≠0)交x轴与A,B两点(点A在点B左侧),将直尺WXYZ与x轴负方向成45°放置,边WZ经过抛物线上的点C(4,m),与抛物线的另一交点为点D,直尺被x轴截得的线段EF=2,且△CEF的面积为6.
(1)求该抛物线的解析式;
(2)探究:在直线AC上方的抛物线上是否存在一点P,使得△ACP的面积最大?若存在,请求出面积的最大值及此时点P的坐标;若不存在,请说明理由.
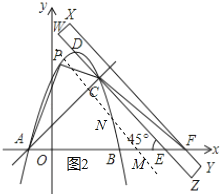
(3)将直尺以每秒2个单位的速度沿x轴向左平移,设平移的时间为t秒,平移后的直尺为W′X′Y′Z′,其中边X′Y′所在的直线与x轴交于点M,与抛物线的其中一个交点为点N,请直接写出当t为何值时,可使得以C、D、M、N为顶点的四边形是平行四边形.
【答案】
(1)
解:∵S△CEF= ![]() EFyC=
EFyC= ![]() ×2m=6,
×2m=6,
∴m=6,即点C的坐标为(4,6),
将点C(4,6)代入抛物线y=ax2+2x+6(a≠0)中,
得:6=16a+8+6,解得:a=﹣ ![]() ,
,
∴该抛物线的解析式为y=﹣ ![]() x2+2x+6
x2+2x+6
(2)
解:假设存在.过点P作y轴的平行线,交x轴与点M,交直线AC于点N,如图1所示.
令抛物线y=﹣ ![]() x2+2x+6中y=0,则有﹣
x2+2x+6中y=0,则有﹣ ![]() x2+2x+6=0,
x2+2x+6=0,
解得:x1=﹣2,x2=6,
∴点A的坐标为(﹣2,0),点B的坐标为(6,0).
设直线AC的解析式为y=kx+b,点P的坐标为(n,﹣ ![]() n2+2n+6)(﹣2<n<4),
n2+2n+6)(﹣2<n<4),
∵直线AC过点A(﹣2,0)、C(4,6),
∴ ![]() ,解得:
,解得: ![]() ,
,
∴直线AC的解析式为y=x+2.
∵点P的坐标为(n,﹣ ![]() n2+2n+6),
n2+2n+6),
∴点N的坐标为(n,n+2).
∵S△ACP= ![]() PN(xC﹣xA)=
PN(xC﹣xA)= ![]() ×(﹣
×(﹣ ![]() n2+2n+6﹣n﹣2)×[4﹣(﹣2)]=﹣
n2+2n+6﹣n﹣2)×[4﹣(﹣2)]=﹣ ![]() (n﹣1)2+
(n﹣1)2+ ![]() ,
,
∴当n=1时,S△ACP取最大值,最大值为 ![]() ,
,
此时点P的坐标为(1, ![]() ).
).
∴在直线AC上方的抛物线上存在一点P,使得△ACP的面积最大,面积的最大值为 ![]() ,此时点P的坐标为(1,
,此时点P的坐标为(1, ![]() )
)
(3)
解:∵直尺WXYZ与x轴负方向成45°放置,
∴设直线CD的解析式为y=﹣x+c,
∵点C(4,6)在直线CD上,
∴6=﹣4+c,解得:c=10,
∴直线CD的解析式为y=﹣x+10.
联立直线CD与抛物线解析式成方程组:  ,
,
解得: ![]() ,或
,或 ![]() ,
,
∴点D的坐标为(2,8).
令直线CD的解析式y=﹣x+10中y=0,则0=﹣x+10,
解得:x=10,即点E的坐标为(10,0),
∵EF=2,且点E在点F的左边,
∴点F的坐标为(12,0).
设点M的坐标为(12﹣2t,0),则点N的坐标为(12﹣2t﹣2,0+2),即N(10﹣2t,2).

∵点N(10﹣2t,2)在抛物线y=﹣ ![]() x2+2x+6的图象上,
x2+2x+6的图象上,
∴﹣ ![]() (10﹣2t)2+2(10﹣2t)+6=2,整理得:t2﹣8t+13=0,
(10﹣2t)2+2(10﹣2t)+6=2,整理得:t2﹣8t+13=0,
解得:t1=4﹣ ![]() ,t2=4+
,t2=4+ ![]() .
.
∴当t为4﹣ ![]() 或4+
或4+ ![]() 秒时,可使得以C、D、M、N为顶点的四边形是平行四边形
秒时,可使得以C、D、M、N为顶点的四边形是平行四边形
【解析】(1)根据三角形的面积公式求出m的值,结合点C的坐标利用待定系数法即可求出a值,从而得出结论;(2)假设存在.过点P作y轴的平行线,交x轴与点M,交直线AC于点N.根据抛物线的解析式找出点A的坐标.设直线AC的解析式为y=kx+b,点P的坐标为(n,﹣ ![]() n2+2n+6)(﹣2<n<4),由点A、C的坐标利用待定系数法即可求出直线AC的解析式,代入x=n,即可得出点N的坐标,利用三角形的面积公式即可得出S△ACP关于n的一元二次函数,根据二次函数的性质即可解决最值问题;(3)根据直尺的摆放方式可设出直线CD的解析式为y=﹣x+c,由点C的坐标利用待定系数法即可得出直线CD的解析式,联立直线CD的解析式与抛物线的解析式成方程组,解方程组即可求出点D的坐标,令直线CD的解析式中y=0,求出x值即可得出点E的坐标,结合线段EF的长度即可找出点F的坐标,设出点M的坐标,结合平行四边形的性质以及C、D点坐标的坐标即可找出点N的坐标,再由点N在抛物线图象上,将其代入抛物线解析式即可得出关于时间t的一元二次方程,解方程即可得出结论.本题考查了三角形的面积公式、待定系数法求函数解析式、二次函数的性质、解二元二次方程组、平行四边形的性质以及解一元二次方程,解题的关键是:(1)求出点C的坐标;(2)利用二次函数的性质解决最值问题;(3)用时间t表示出来点N的坐标.本题属于中档题,难度不大,但较繁琐,解决该题型题目时,联立函数解析式成方程组,解方程组求出交点坐标是关键.
n2+2n+6)(﹣2<n<4),由点A、C的坐标利用待定系数法即可求出直线AC的解析式,代入x=n,即可得出点N的坐标,利用三角形的面积公式即可得出S△ACP关于n的一元二次函数,根据二次函数的性质即可解决最值问题;(3)根据直尺的摆放方式可设出直线CD的解析式为y=﹣x+c,由点C的坐标利用待定系数法即可得出直线CD的解析式,联立直线CD的解析式与抛物线的解析式成方程组,解方程组即可求出点D的坐标,令直线CD的解析式中y=0,求出x值即可得出点E的坐标,结合线段EF的长度即可找出点F的坐标,设出点M的坐标,结合平行四边形的性质以及C、D点坐标的坐标即可找出点N的坐标,再由点N在抛物线图象上,将其代入抛物线解析式即可得出关于时间t的一元二次方程,解方程即可得出结论.本题考查了三角形的面积公式、待定系数法求函数解析式、二次函数的性质、解二元二次方程组、平行四边形的性质以及解一元二次方程,解题的关键是:(1)求出点C的坐标;(2)利用二次函数的性质解决最值问题;(3)用时间t表示出来点N的坐标.本题属于中档题,难度不大,但较繁琐,解决该题型题目时,联立函数解析式成方程组,解方程组求出交点坐标是关键.
【考点精析】掌握二次函数的性质和三角形的面积是解答本题的根本,需要知道增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;三角形的面积=1/2×底×高.

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案【题目】达州市图书馆今年4月23日开放以来,受到市民的广泛关注.5月底,八年级(1)班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计,并制成了如图不完整的统计图表.
八年级(1)班学生去新图书馆的次数统计表
去图书馆的次数 | 0次 | 1次 | 2次 | 3次 | 4次及以上 |
人数 | 8 | 12 | a | 10 | 4 |
请你根据统计图表中的信息,解答下列问题:
(1)填空:a= , b=;
(2)求扇形统计图中“0次”的扇形所占圆心角的度数;
(3)从全班去过该图书馆的同学中随机抽取1人,谈谈对新图书馆的印象和感受.求恰好抽中去过“4次及以上”的同学的概率.









