题目内容
【题目】如图,在平面直角坐标系中,边长为1的正方形OA1B1C1的两边在坐标轴上,以它的对角线OB1为边作正方形OB1B2C2 , 再以正方形OB1B2C2的对角线OB2为边作正方形OB2B3C3 , 以此类推…、则正方形OB2015B2016C2016的顶点B2016的坐标是 . 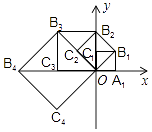
【答案】(21008 , 0)
【解析】解:∵正方形OA1B1C1边长为1,
∴OB1= ![]() ,
,
∵正方形OB1B2C2是正方形OA1B1C1的对角线OB1为边,
∴OB2=2,
∴B2点坐标为(0,2),
同理可知OB3=2 ![]() ,
,
∴B3点坐标为(﹣2,2),
同理可知OB4=4,B4点坐标为(﹣4,0),
B5点坐标为(﹣4,﹣4),B6点坐标为(0,﹣8),
B7(8,﹣8),B8(16,0)
B9(16,16),B10(0,32),
由规律可以发现,每经过8次作图后,点的坐标符号与第一次坐标符号相同,每次正方形的边长变为原来的 ![]() 倍,
倍,
∵2016÷8=252
∴B2016的纵横坐标符号与点B8的相同,横坐标为正值,纵坐标是0,
∴B2016的坐标为(21008 , 0).
故答案为:(21008 , 0).
首先求出B1、B2、B3、B4、B5、B6、B7、B8、B9的坐标,找出这些坐标的之间的规律,然后根据规律计算出点B2016的坐标.

练习册系列答案
相关题目
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数 | 60≤x<90 | 90≤x<120 | 120≤x<150 | 150≤x<180 | 180≤x<210 |
频数 | 16 | 25 | 9 | 7 | 3 |
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几(精确到0.1%)?