题目内容
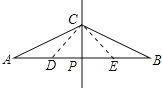
【题目】如图，已知线段AB的垂直平分线CP交AB于点P，且AP=2PC，现欲在线段AB上求作两点D，E，使其满足AD=DC=CE=EB，对于以下甲、乙两种作法：
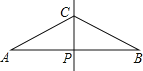
甲：分别作∠ACP、∠BCP的平分线，分别交AB于D、E，则D、E即为所求；乙：分别作AC、BC的垂直平分线，分别交AB于D、E，则D、E两点即为所求．下列说法正确的是（ ）
A. 甲、乙都正确 B. 甲、乙都错误
C. 甲正确，乙错误 D. 甲错误，乙正确
【答案】D
【解析】试题解析：甲：虽然CP=
AP，
但∠A≠
∠ACP，
即∠A≠∠ACD．甲不正确；
乙∵CP是线段AB的中垂线，
∴△ABC是等腰三角形，即AC=BC，∠A=∠B，
作AC、BC之中垂线分别交AB于D、E，
∴∠A=∠ACD，∠B=∠BCE，
∵∠A=∠B，
∴∠A=∠ACD，∠B=∠BCE，
∵AC=BC，
∴△ACD≌△BCE，
∴AD=EB，
∵AD=DC，EB=CE，
∴AD=DC=EB=CE．乙正确，
故选D．
练习册系列答案
应用题天天练四川大学出版社系列答案
相关题目
