题目内容
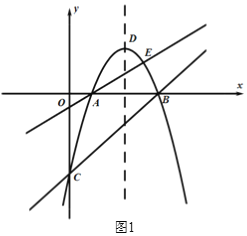
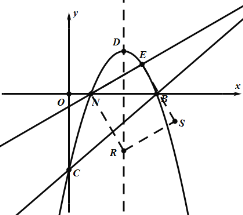
【题目】如图1,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线AE:
与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线AE:![]() 与抛物线相交于另一点E,点D为抛物线的顶点.
与抛物线相交于另一点E,点D为抛物线的顶点.
(1)求直线BC的解析式及点E的坐标;
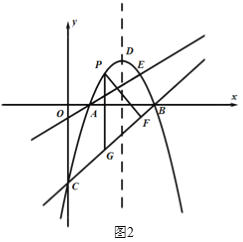
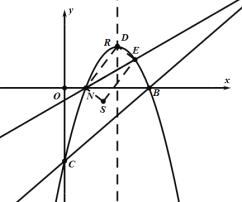
(2)如图2,直线AE上方的抛物线上有一点P,过点P作PF⊥BC于点F,过点P作平行于![]() 轴的直线交直线BC于点G,当△PFG周长最大时,在
轴的直线交直线BC于点G,当△PFG周长最大时,在![]() 轴上找一点M,在AE上找一点N,使得
轴上找一点M,在AE上找一点N,使得![]() 值最小,请求出此时N点的坐标及
值最小,请求出此时N点的坐标及![]() 的最小值;
的最小值;
(3)在第(2)问的条件下,点R为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点N,E,R,S为顶点的四边形为矩形,若存在,请直接写出点S的坐标,若不存在,请说明理由.
【答案】(1)![]() ;E(
;E(![]() ,
,![]() );(2)N(1,0);最小值为
);(2)N(1,0);最小值为![]() ;
;
(3)S1(![]() ,
,![]() ),S2(
),S2(![]() ,
,![]() ),S3(
),S3(![]() ,
,![]() ),S4(
),S4(![]() ,
,![]() )
)
【解析】
(1)首先求出B、C两点坐标,利用待定系数法即可求出直线BC的解析式,联立方程即可求出点E的坐标.
(2)由△PGF∽△OBC可得:![]() ,则
,则![]() ,当PG取最大值时,△PFG周长最大,设
,当PG取最大值时,△PFG周长最大,设![]() ,进而表示出
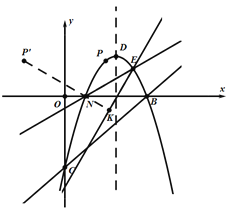
,进而表示出![]() ,根据二次函数最值的求法即可求出点P的坐标,作点P关于
,根据二次函数最值的求法即可求出点P的坐标,作点P关于![]() 轴的对称点P′,将直线AE绕点E逆时针方向旋转
轴的对称点P′,将直线AE绕点E逆时针方向旋转![]() °得直线
°得直线![]() ,且满足
,且满足![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点K,交直线AE于点N,此时
于点K,交直线AE于点N,此时![]() 最小,求解即可.
最小,求解即可.
(3)分四种情况,分别画出示意图,求解即可.
解:(1)由抛物线解析式得B(4,0),C(0,-2![]() ),
),
设直线BC解析式为:![]() ,代入B、C坐得:
,代入B、C坐得:![]() ,
,
∴![]() ,
,![]() ,
,
∴BC解析式为:![]() ,
,
联立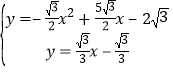 ,
,
解得![]() ;
;
(2)由△PGF∽△OBC可得:![]() ,
,
∴![]() ,
,
∴当PG取最大值时,△PFG周长最大,
设![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∵对称轴为直线a=2,开口向下,
∴当![]() 时,PG取得最大值,即△PFG周长最大,此时P(2,
时,PG取得最大值,即△PFG周长最大,此时P(2,![]() ),
),
作点P关于![]() 轴的对称点P′(2,-
轴的对称点P′(2,-![]() ),
),
将直线AE绕点E逆时针方向旋转![]() °得直线
°得直线![]() ,且满足
,且满足![]() ,
,
过点![]() 作直线
作直线![]() 的垂线交
的垂线交![]() 于点K,交直线AE于点N,
于点K,交直线AE于点N,
此时![]() 最小,
最小,
∴直线![]() 解析式为
解析式为![]() ,
,
直线![]() 的解析式为
的解析式为![]() ,
,
∴N点坐标为(1,0),
K点坐标为![]() ,
,
∴![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,![]() .
.

【题目】某公司生产A种产品,它的成本是6元/件,售价是8元/件,年销售量为5万件.为了获得更好的效益,公司准备拿出一定的资金做广告,根据经验,每年投入的广告费是x万元,产品的年销售量将是原销售量的y倍,且y与x之间满足我们学过的二种函数(即一次函数和二次函数)关系中的一种,它们的关系如下表:
x(万元) | 0 | 0.5 | 1 | 1.5 | 2 | … |
y | 1 | 1.275 | 1.5 | 1.675 | 1.8 | … |
(1)求y与x的函数关系式(不要求写出自变量的取值范围)
(2)如果把利润看作是销售总额减去成本费用和广告费用,试求出年利润W(万元)与广告费用x(万元)的函数关系式,并计算每年投入的广告费是多少万元时所获得的利润最大?
(3)如果公司希望年利润W(万元)不低于14万元,请你帮公司确定广告费的范围.