题目内容
【题目】用一定数目的点或大小相同的圆在等距离的排列下可以形成一个等边三角形数阵.古希腊著名数学家毕达哥拉斯用数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ……这些数量的(石子),都成功的排成了等边三角形数阵..
……这些数量的(石子),都成功的排成了等边三角形数阵..
(问题提出)![]() 结果等于多少?
结果等于多少?
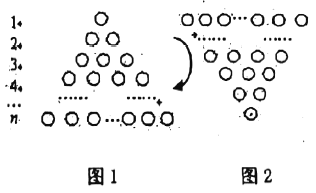
在图1所示的等边三角形数阵中,前![]() 行有
行有![]() 个圆圈,前
个圆圈,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,前
,前![]() 行有
行有![]() 个圆圈,即
个圆圈,即![]() ,…,则前
,…,则前![]() 行所有圆圈个数总和为
行所有圆圈个数总和为![]()
将图1旋转至图2,观察这两个三角形数阵中同一行圆圈个数(如第![]() 行的圆圈个数分别为
行的圆圈个数分别为![]() 个,
个,![]() 个),发现同一行圆圈个数之和均为___________个,由此可得两个图前
个),发现同一行圆圈个数之和均为___________个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(问题延伸)![]() 结果等于多少?
结果等于多少?
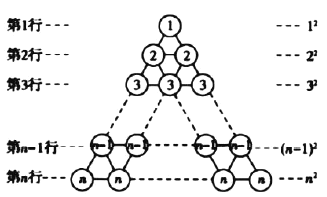
图3
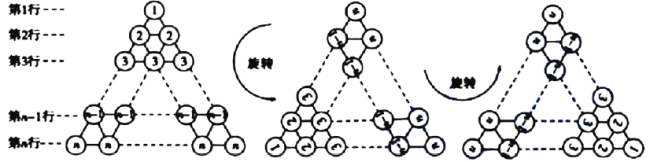
图4
在图3所示的等边三角形数阵中,第![]() 行圆圈中的数为
行圆圈中的数为![]() ,即
,即![]() ,第
,第![]() 行两个圆圈中数字的和为
行两个圆圈中数字的和为![]() .即
.即![]() …,第
…,第![]() 行
行![]() 个圆圈中数字的和为
个圆圈中数字的和为![]() (共
(共![]() 个).即
个).即![]() .这样,该三角形数阵中所有圆圈中数字的和为
.这样,该三角形数阵中所有圆圈中数字的和为![]() .
.
将该三角形数阵经两次旋转可得如图4所示的三个三角形数阵,观察这三个三角形数阵中各行同一位置上圆圈中的数字(如第![]() 行的第一个圆圈中的数字分别为
行的第一个圆圈中的数字分别为![]() ,
,![]() ,
,![]() ),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
),发现相同位置上三个圆圈中数字之和均为___________,由此可得,这三个三角形数阵所有圆圈中数字的总和为:![]() ___________,因此,
___________,因此,![]() ___________.
___________.
(规律应用)
根据以上发现,计算:![]() 的结果为___________.
的结果为___________.
【答案】(问题提出)n+1;n(n+1);![]() ;(问题延伸)2n+1;
;(问题延伸)2n+1; ![]() ×(2n+1);
×(2n+1);![]() (规律应用)1345.
(规律应用)1345.
【解析】
(问题提出)根据图形可发现同一行圆圈个数之和均为(n+1)个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() n(n+1),因此可求出
n(n+1),因此可求出![]() ;
;
(问题延伸)根据材料可得相同位置上三个圆圈中数字之和为![]() +
+![]() +
+![]() =2n+1,由此可得,这三个三角形数阵所有圆圈中数字的总和为:
=2n+1,由此可得,这三个三角形数阵所有圆圈中数字的总和为:![]()
![]() ×(2n+1),因此变形即可求出
×(2n+1),因此变形即可求出![]() ;
;
(规律应用)根据规律即可化简求解.
(问题提出)观察这两个三角形数阵中同一行圆圈个数(如第![]() 行的圆圈个数分别为
行的圆圈个数分别为![]() 个,
个,![]() 个),发现同一行圆圈个数之和均为(n+1)个,由此可得两个图前
个),发现同一行圆圈个数之和均为(n+1)个,由此可得两个图前![]() 行圆圈个数总和为:
行圆圈个数总和为:![]() n(n+1),因此,
n(n+1),因此,![]()
![]() ,
,
故答案为:n+1;n(n+1);![]() ;
;
(问题延伸)
∵![]() +
+![]() +
+![]() =2n+1,
=2n+1,
∴相同位置上三个圆圈中数字之和为![]() +
+![]() +
+![]() =2n+1,
=2n+1,
∴这三个三角形数阵所有圆圈中数字的总和为:![]()
![]() ×(2n+1),
×(2n+1),
∴![]() =
=![]()
故答案为:2n+1; ![]() ×(2n+1);
×(2n+1);![]()
(规律应用)![]()
=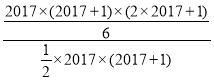
=![]()
=1345
故答案为:1345.

【题目】某大学举行了百科知识竞赛,为了解此次竞赛成绩的情况,随机抽取部分参赛学生的成绩,整理并制作出如下不完整的统计表和统计图,请根据图表信息解答以下问题:
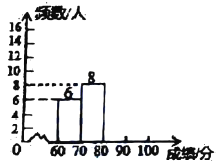

组别 | 成绩 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
(1)表中![]() ___________.
___________.
(2)补全频数分布直方图
(3)计算扇形统计图中“![]() ”对应的圆心角度数.
”对应的圆心角度数.
(4)该大学共有![]() 人参加竞赛,若成绩在
人参加竞赛,若成绩在![]() 分以上(包括
分以上(包括![]() 分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.
分)的为“优”等,根据抽样结果,估计该校参赛学生成绩达到“优”等的人数.