题目内容
如图,直径为5的⊙M圆心在x轴正半轴上,⊙M和x轴交于A、B两点,和y轴交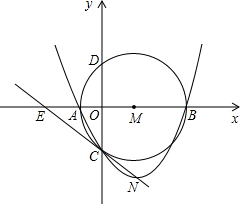 于C、D两点且CD=4,抛物线y=ax2+bx+c经过A、B、C三点,顶点为N﹒
于C、D两点且CD=4,抛物线y=ax2+bx+c经过A、B、C三点,顶点为N﹒
(1)求经过A、B、C三点的抛物线解析式;
(2)直线NC与x轴交于点E,试判断直线CN与⊙M的位置关系并说明理由;
(3)设点Q是(1)中所求抛物线对称轴上的一点,试问在(1)中所求抛物线上是否存在点P使以点A、B、P、Q为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,请说明理由﹒
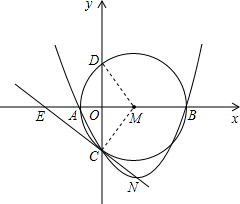 解:(1)连接DM,∵⊙M的直径5,
解:(1)连接DM,∵⊙M的直径5,∴DM=
 ,
,∵CD=4,
∴OD=0C=2,
∴C点的坐标为(0,-2),
∴OM=
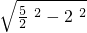 =
= ,
,∴OA=
 -
- =1,
=1,∴OB=5-OA=4,
∴点A的坐标为(-1,0),点B的坐标为(4,0)
由A、B两点坐标,设抛物线y=a(x+1)(x-4),将C(0,-2)代入,得a=
 ,
,∴y=
 (x+1)(x-4),
(x+1)(x-4),∴经过A、B、C三点的抛物线解析式为y=
 x2-
x2- x-2;
x-2;(2)直线CN与⊙M相切;
连接CM,设过CN直线的解析式为y=kx+b,
设抛物线的顶点为N,则N点的坐标为(
 ,-
,- ),
),∴CN直线的解析式为y=-
 x-2,
x-2,∴点E的坐标为(-
 ,0),
,0),∴CE=
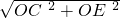 =
= ,
,∴EM=OE+OM=
 ,
,∵CM2=
 ,CE2=
,CE2= ,EM2=
,EM2=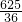 ,
,∴CM2+CE2=EM2,
∴△ECM是直角三角形,即MC⊥EC,
∴直线CN与⊙M相切;
(3)存在符合条件的点P,
当AB为平行四边形的一边时,PQ∥AB,PQ=AB=5,P点横坐标为
 +5=
+5= 或
或 -5=-
-5=- ,
,分别代入抛物线解析式,得y=
 ,
,当AB为平行四边形的对角线时,P为抛物线顶点,
∴P点的坐标是(
 ,-
,- ),(-
),(- ,
,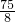 ),(
),( ,
,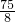 ).
).分析:(1)若要求经过A、B、C三点的抛物线解析式,则可求出A、B、C三点的坐标即可;
(2)连接MC,再证明CM⊥EN即可;
(3)存在,根据AB为平行四边形的边,对角线两种情况,分别P点坐标.
点评:此题考查待定系数法求函数解析式,二次函数的对称性,以及平行四边和圆的切线的有关知识的运用,是一道综合性很强的题目,难度较大.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目

 长交y轴于点D(0,3)
长交y轴于点D(0,3)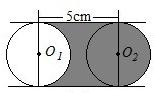 12、如图,直径为4cm的⊙O1平移5cm到⊙O2,则图中阴影部分面积为
12、如图,直径为4cm的⊙O1平移5cm到⊙O2,则图中阴影部分面积为 如图,直径为2的两圆⊙O1和⊙O2均与y轴相切于点O,反比例函数
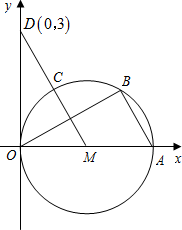
如图,直径为2的两圆⊙O1和⊙O2均与y轴相切于点O,反比例函数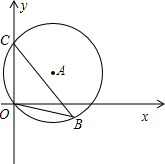 (2012•枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )
(2012•枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( ) 如图,直径为1的圆上有一点A与数轴上的原点O重合,若该圆向左滚动一周,则点A表示的数为
如图,直径为1的圆上有一点A与数轴上的原点O重合,若该圆向左滚动一周,则点A表示的数为