题目内容
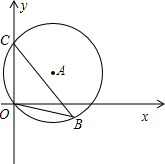 (2012•枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )
(2012•枣庄)如图,直径为10的⊙A经过点C(0,5)和点O(0,0),B是y轴右侧⊙A优弧上一点,则cos∠OBC的值为( )分析:连接CD,由∠COD为直角,根据90°的圆周角所对的弦为直径,可得出CD为圆A的直径,再利用同弧所对的圆周角相等得到∠CBO=∠CDO,在直角三角形OCD中,由CD及OC的长,利用勾股定理求出OD的长,然后利用余弦函数定义求出cos∠CDO的值,即为cos∠CBO的值.
解答: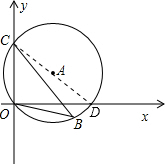 解:连接CD,如图所示:
解:连接CD,如图所示:
∵∠COD=90°,
∴CD为圆A的直径,即CD过圆心A,
又∵∠CBO与∠CDO为
所对的圆周角,
∴∠CBO=∠CDO,
又∵C(0,5),
∴OC=5,
在Rt△CDO中,CD=10,CO=5,
根据勾股定理得:OD=
=5
,
∴cos∠CBO=cos∠CDO=
=
=
.
故选B
 解:连接CD,如图所示:
解:连接CD,如图所示:∵∠COD=90°,
∴CD为圆A的直径,即CD过圆心A,
又∵∠CBO与∠CDO为
 |
| CO |
∴∠CBO=∠CDO,
又∵C(0,5),
∴OC=5,
在Rt△CDO中,CD=10,CO=5,
根据勾股定理得:OD=
| CD2-OC2 |
| 3 |
∴cos∠CBO=cos∠CDO=
| OD |
| CD |
5
| ||
| 10 |
| ||
| 2 |
故选B
点评:此题考查了圆周角定理,勾股定理,坐标与图形性质,以及锐角三角函数定义,熟练掌握定理是解本题的关键.

练习册系列答案
相关题目
 (2012•枣庄)如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )
(2012•枣庄)如图是每个面上都有一个汉字的正方体的一种侧面展开图,那么在原正方体的表面上,与汉字“美”相对的面上的汉字是( )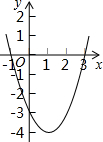 (2012•枣庄)二次函数y=x2-2x-3的图象如图所示.当y<0时,自变量x的取值范围是
(2012•枣庄)二次函数y=x2-2x-3的图象如图所示.当y<0时,自变量x的取值范围是 (2012•枣庄)如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若AB的长为8cm,则图中阴影部分的面积为
(2012•枣庄)如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若AB的长为8cm,则图中阴影部分的面积为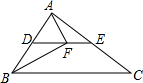 (2012•枣庄)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为
(2012•枣庄)如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=5,BC=8,则EF的长为