Question

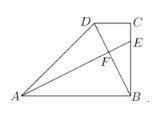
【题目】如图，在梯形中，，，，，，，垂足为点.

（1）求的余弦值；

（2）设，，用向量、表示.

Answer 1

【答案】（1）；（2）

【解析】

(1)作DM⊥AB，垂足为M，易得：DM=AM=4，AD=4，BC=DM=4，从而得tan∠BAE=，设BF=x，则AF=2x，根据勾股定理，即可求解；

(2)易得：，，根据，即可求解.

（1）作DM⊥AB，垂足为M，

∵在梯形中，，，

∴四边形BCDM是矩形，

∴BM=CD=2，AM=AB-BM=6-2=4，

∵，

∴AMD是等腰直角三角形，

∴DM=AM=4，AD=4，BC=DM=4，

∴tan∠CBD=，

∵，

∴∠BEF+∠EBF=90°，

∵∠BEF+∠BAE=90°，

∴∠EBF =∠BAE，

∴tan∠BAE=，

设BF=x，则AF=2x，

∵在RtABF中，，

∴，解得：x=，

∴AF=2x=，

∴的余弦值=；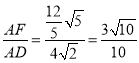

（2）∵AB=6，tan∠BAE=，

∴BE=3，

∵BC=4，

∴BE=，即： ，

∵CD=2，AB=6, ，

∴，

∵.