题目内容
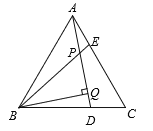
【题目】(1)如图1,在△ABC中,∠ACB=90°,AC=BC,直线l过点C,点A,B在直线l同侧,BD⊥l,AE⊥l,垂足分别为D,E.求证:△AEC≌△CDB.
(2)如图2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的结论,请按照图中所标注的数据计算图中实线所围成的图形的面积S= .
【答案】(1)见解析;(2)S= 50.
【解析】
(1)因为BD⊥l,AE⊥l,可得∠AEC=∠CDB,结合题意得到∠CAE=∠BCD,再根据AAS证明即可.
(2)利用(1)中结论,根据全等三角形的性质进行计算即可解决问题.
(1)如图1中,
∵BD⊥l,AE⊥l,
∴∠AEC=∠CDB=90°,
∴∠CAE+∠ACE=90°,
∴∠BCD+∠ACE=90°,
∴∠CAE=∠BCD,
在△AEC和△CDB中
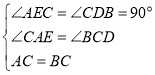 ,
,
∴△AEC≌△CDB(AAS).
(2)如图2中,因为AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,
由(1)可知:△EFA≌△AGB,△BGC≌△CHD,
∴EF=AG=6,AF=BG=CH=3,CG=DH=4,
∴S=![]() (6+4)×16-18-12=50.
(6+4)×16-18-12=50.
故答案为50.

练习册系列答案
相关题目
【题目】某学校为了解本校八年级学生生物考试测试情况,随机抽取了本校八年级部分学生的生物测试成绩为样本,按A(优秀)、B(良好)、C(合格)、D(不合格)四个等级进行统计,并将统计结果绘制成如下统计图表.请你结合图表中所给信息解答下列问题:
等级 | 人数 |
A(优秀) | 40 |
B(良好) | 80 |
C(合格) | 70 |
D(不合格) |
(1)请将上面表格中缺少的数据补充完整;
(2)扇形统计图中“A”部分所对应的圆心角的度数是 ;
(3)该校八年级共有1200名学生参加了身体素质测试,试估计测试成绩合格以上(含合格)的人数.