题目内容
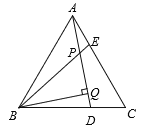
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
【答案】(1)见解析;(2)PE=1.
【解析】
(1)根据等边三角形的性质得到AB=AC,∠BAE=∠C=60°,证明△ABE≌△CAD
(2)根据直角三角形的性质得到BP=2PQ,再根据题意BP=2PQ =4,则PE =1.
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,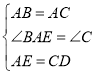 ,
,
∴△ABE≌△CAD(SAS),
(2) ∵△ABE≌△CAD,
∴∠ABE=∠CAQ,
∴∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=∠BAC=60°,∵BQ⊥AD,
∴∠PBQ=90°∠BPQ=90°60°=30°,
∴BP=2PQ.
∵PQ=2,BE=5,
则BP=2PQ =4,PE = BE- PB=5-4=1.

练习册系列答案
相关题目
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
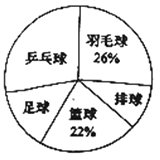
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.