题目内容
【题目】如图,已知抛物线y=![]() +bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB,AC分别交于点E,F,当四边形AECP的面积最大时,求点P的坐标.
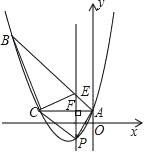
【答案】(1) y=![]() x2+2x+1,(2) P(﹣
x2+2x+1,(2) P(﹣![]() ,﹣
,﹣![]() ).
).
【解析】试题分析:(1)用待定系数法求出抛物线解析式即可;
(2)设点![]() 表示出
表示出![]() 再用S四边AECP=S△AEC+S△APC建立函数关系式,求出最大值即可.
再用S四边AECP=S△AEC+S△APC建立函数关系式,求出最大值即可.
试题解析:(1)∵点A(0,1).B(9,10)在抛物线上,
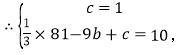
![]()
∴抛物线的解析式为![]()
(2)∵AC∥x轴,A(0,1)
∴![]()
![]()
∴点C的坐标(6,1),
∵点A(0,1).B(9,10),
∴直线AB的解析式为y=x+1,
设点![]()
∴E(m,m+1)
∴![]()
∵AC⊥EP,AC=6,
∴S四边AECP=S△AEC+S△APC
![]()
![]()
∵6<m<0
∴当![]() 时,四边形AECP的面积的最大值是
时,四边形AECP的面积的最大值是![]()
此时点![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
平均分(分) | 中位数(分) | 众数(分) | 方差( | |
初中部 | a | 85 | b |
|
高中部 | 85 | c | 100 | 160 |
(1)根据图示计算出a、b、c的值;
(2)结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?
(3)计算初中代表队决赛成绩的方差![]() ,并判断哪一个代表队选手成绩较为稳定.
,并判断哪一个代表队选手成绩较为稳定.

【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.

组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.