Question

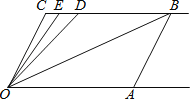
【题目】如图，D,E,F,G,H,I是三角形ABC三边上的点，连结EI，EF∥BC, GH∥AC, DI∥AB.

(1)写出与∠IEC是同旁内角的角。

(2)判断∠GHC与∠FEC是否相等，并说明理由。

(3)若EI平分∠FEC，∠C=56°，∠B=50°，求∠EID的度数。

Answer 1

【答案】（1）与∠IEC是同旁内角的角是：∠C、∠EDI、∠EIC、∠EID ，（2）∠GHC=∠FEC ，理由见解析，（3）12°.

【解析】

试题分析：（1）根据同旁内角的定义确定即可；（2）利用平行线的性质得出∠FEC+∠C=180°和∠GHC+∠C=180°，再利用补角的性质即可得出结论；（3）利用平行线的性质得出∠FEC=180°-∠C=124°，∠DIC=∠B=50°，利用角的平分线得出∠FEI=∠FEC=62°，然后利用角的和差关系即可得出结论.

试题解析：（1）与∠IEC是同旁内角的角是：∠C、∠EDI、∠EIC、∠EID

（2）∠GHC=∠FEC

理由：∵EF∥BC

∴∠FEC+∠C=180°

∵GH∥AC

∴∠GHC+∠C=180°

∴∠GHC=∠FEC

(3) ∵EF∥BC,∠C=56°

∴∠FEC+∠C=180°

∴∠FEC=180°-∠C=124°

∵EI平分∠FEC

∴∠FEI=∠FEC=62°

∴∠FEI=∠EIC=62°

∵DI∥AB,∠B=50°

∴∠DIC=∠B=50°

∴∠EID=∠EIC-∠DIC=12°