题目内容
13.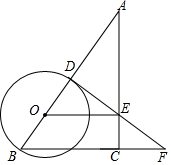 如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F.
如图,在Rt△ABC中,∠ACB=90°,点O是AB上的动点,⊙O过点B交AB于点D,OE⊥AC,垂足为E,DE的延长线交BC的延长线于点F.(1)若BC=3,AC=4,当DE与⊙O相切时,求⊙O的半径;
(2)当BF=BD时,AC是⊙O的切线吗?为什么?
分析 (1)根据勾股定理得到AB=5,由DE与⊙O相切,得到∠ODE=90°,推出△ODE∽△ABC,根据相似三角形的性质得到OE=$\frac{5r}{3}$,OE=$\frac{15-3r}{5}$,于是列方程得到结论;
(2)根据相似三角形的性质得到$\frac{OD}{BD}$=$\frac{OE}{BF}$,根据分式的性质得到OE=OD,然后根据切线的判定定理即可得到结论.
解答 解:(1)∵∠ACB=90°,BC=3,AC=4,
∴AB=5,
∵DE与⊙O相切,
∴∠ODE=90°,
∴∠ACB=∠ODE,
∵OE⊥AC,
∴OE∥BC,
∴∠DOE=∠B,
∴△ODE∽△ABC,
∴$\frac{OE}{AB}=\frac{OD}{BC}$,
设⊙O的半径为r,
∴$\frac{OE}{5}=\frac{r}{3}$,
∴OE=$\frac{5r}{3}$,
∵OE∥BC,
∴△AOE∽△ABC,
∴$\frac{OE}{BC}$=$\frac{AO}{AB}$,
∴$\frac{OE}{3}$=$\frac{5-r}{5}$,
∴OE=$\frac{15-3r}{5}$,
∴$\frac{5r}{3}$=$\frac{15-3r}{5}$,
∴r=$\frac{45}{34}$;
(2)AC是⊙O的切线,
理由:∵OE∥BF,
∴△DOE∽△DBF,
∴$\frac{OD}{BD}$=$\frac{OE}{BF}$,
∵BD=BF,
∴OE=OD,
∵OE⊥AC,
∴AC是⊙O的切线.
点评 本题考查了切线的判定和性质,相似三角形的判定和性质,勾股定理.熟练掌握切线的判定和性质是解题的关键.

练习册系列答案
相关题目
3.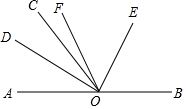 如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )
如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )
 如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )
如图,O为直线AB上一点,过点O作直线OC,若∠AOC为锐角,射线OD平分∠AOC,射线OE平分∠BOC,射线OF平分∠DOE,则∠FOB+∠DOC的度数为( )| A. | 100° | B. | 110° | C. | 120° | D. | 135° |
20.已知圆锥的母线长为5cm,高为4cm,则这个圆锥的侧面积为( )
| A. | 12π cm2 | B. | 15π cm2 | C. | 20π cm2 | D. | 25π cm2 |
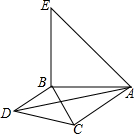 已知,如图,在△ABC中,∠BAC=45°,以B为直角顶点分别作Rt△BCD、Rt△BAE,且BC=BD,BA=BE,连接AD.猜想并证明线段AB、AD、AC之间的数量关系.
已知,如图,在△ABC中,∠BAC=45°,以B为直角顶点分别作Rt△BCD、Rt△BAE,且BC=BD,BA=BE,连接AD.猜想并证明线段AB、AD、AC之间的数量关系.