题目内容
我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离;即|x|=|x-0|,也就是说,|x|表示在数轴上数x与数0对应点之间的距离;这个结论可以推广为|x1-x2|表示在数轴上x1,x2对应点之间的距离;
例1解方程|x|=2,容易看出,在数轴下与原点距离为2点的对应数为±2,即该方程的解为x=±2
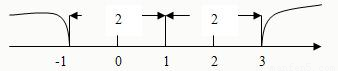
例2解不等式|x-1|>2,如图,在数轴上找出|x-1|>2的解,即到1的距离为2的点对应的数为-1、3,则|x-1|>2的解为x<-1或X>3
参考阅读材料,解答下列问题:
不等式|x+3|>4的解为 .
【答案】分析:不等式|x+3|>4可写成|x-(-3)|>4,则就是到-3点的距离等于4有-7和1.
解答:解:
∵|x+3|=|x-(-3)|>4,
即到-3的距离为4的点对应的数为-7、1,
用数轴表示为:
∴不等式|x+3|>4的解为x<-7或x>1.
点评:不等式的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
解答:解:
∵|x+3|=|x-(-3)|>4,
即到-3的距离为4的点对应的数为-7、1,
用数轴表示为:

∴不等式|x+3|>4的解为x<-7或x>1.
点评:不等式的解集在数轴上表示的方法:把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
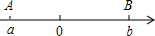
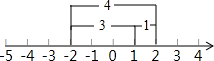 x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题:
x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题: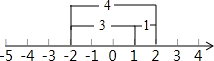 x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题:
x的对应点在-2的左边,可得x=-3,所以原方程的解是x=2或x=-3.根据上面的阅读材料,解答下列问题: