题目内容
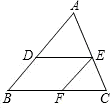如图，DE∥BC，EF∥AB，∠ADE=75°，则∠BFE=
- A.75°
- B.105°
- C.44°
- D.46°
B
分析：由DE∥BC，根据平行线的性质能求出∠B的度数，再由EF∥AB，推出∠B+∠BFE=180°，即可求出∠BFE的度数．
解答：∵DE∥BC，∠ADE=75°，
∴∠ADE=∠B=75°，
∵EF∥AB，
∴∠B+∠BFE=180°，
∴∠BFE=180°-75°=105°．
故选B．
点评：本题主要考查了对平行线的性质的理解和掌握，题型较好，比较典型．
分析：由DE∥BC，根据平行线的性质能求出∠B的度数，再由EF∥AB，推出∠B+∠BFE=180°，即可求出∠BFE的度数．
解答：∵DE∥BC，∠ADE=75°，
∴∠ADE=∠B=75°，
∵EF∥AB，
∴∠B+∠BFE=180°，
∴∠BFE=180°-75°=105°．
故选B．
点评：本题主要考查了对平行线的性质的理解和掌握，题型较好，比较典型．
练习册系列答案
字词句段篇系列答案
相关题目
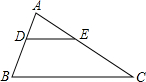如图，DE∥BC，且DB=AE，若AB=5，AC=10，则AE的长为
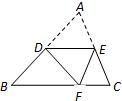12、如图，DE∥BC，将△ABC沿DE所在的直线折叠，点A正好落在BC边上F处，若∠B=40°，则∠BDF=
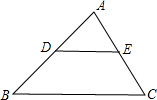如图，DE∥BC，AD：DB=3：4，则△ADE与△ABC的周长之比为
（1997•广西）如图，DE∥BC，AB=15，AC=9，BD=4，那么AE=（ ）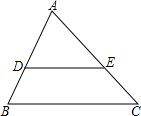
（1997•河北）已知：如图，DE∥BC，AD=3.6，DB=2.4，AC=7．求EC的长．