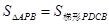题目内容
如图所示,在梯形ABCD中,AD∥BC,∠BDC=90°,E为DC上一点,∠BDE=∠DBC.

(1)求证:DE=CE;
(2)若 ,试判断四边形ABED的形状,并说明理由.
,试判断四边形ABED的形状,并说明理由.

(1)求证:DE=CE;
(2)若
 ,试判断四边形ABED的形状,并说明理由.
,试判断四边形ABED的形状,并说明理由.(1)证明见解析;(2)四边形ABED为菱形,理由见解析.
试题分析:(1)由∠BDC=90°,∠BDE=∠DBC,利用等角的余角相等,即可得∠EDC =∠C,又由等角对等边,即可证得DE=EC.
(2)先证四边形ABED是平行四边形,由BE=DE,即可证得四边形ABED为菱形.
试题解析:(1)∵∠BDC=90°,∴∠BDE+∠EDC=90°,且∠DBC+∠C=90°.
又∵∠BDE=∠DBC,∴∠EDC =∠C. ∴DE=EC.
(2)四边形ABED为菱形,理由如下:
∵∠BDE=∠DBC,∴BE=DE.
∵DE=EC,∴
 .
.∵
 ,∴AD=BE.
,∴AD=BE.又∵AD∥BC,∴四边形ABED为平行四边形.
又∵BE=DE,∴
 为菱形.
为菱形.
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目



 中,
中, ,E为
,E为 的中点,求∠
的中点,求∠ 的度数.
的度数.