题目内容
【题目】教材呈现：下图是华师版九年级上册数学教材第77页的部分内容.
猜想
如图，在△ABC中，点D、E分别是AB与AC的中点，根据画出的图形，可以猜想：
DE∥BC，且DE＝
BC．
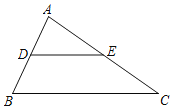
对此，我们可以用演绎推理给出证明
证明在△ABC中，
∵点D、E分别是AB与AC的中点，
∴
请根据教材提示，结合图①，写出完整证明过程，
结论应用：
如图②在四边形ABCD中，AD＝BC，点P是对角线BD的中点，M是DC中点，N是AB中点，MN与BD相交于点Q．
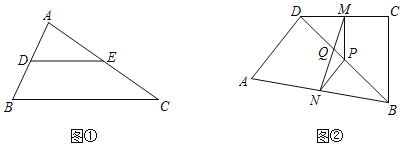
（1）求证：∠PMN＝∠PNM；
（2）若AD＝BC＝4，∠ADB＝90°，∠DBC＝30°，则PQ＝ ．
【答案】教材呈现：证明见解析；结论应用：（1）证明见解析；（2）
．
【解析】
教材呈现：先判断出△ADE∽△ABC，即可得出绪论；
结论应用：（1）根据教材呈现中的续签，得出PM＝
BC，PN＝AD，再利用BC＝AD，即可得出绪论；
（2）先根据（1）的结论判断出∠MPN＝120°，进而求得∠PMN＝∠PNM＝30°，∠EPQ＝30°，再利用三角函数求解即可得出结论.
教材呈现：
在△ABC中，
∵点D、E分别是AB与AC的中点，
∴
，
∵∠A＝∠A，
∴△ADE∽△ABC，
∴DE∥BC，
，
即：DE∥BC，DE＝BC，
结论应用：
（1）证明：∵点P，M分别是BD，DC的中点，
∴PM＝BC，
∵点P，N分别是BD，AB的中点，
∴PN＝AD，
∵BC＝AD，
∴PM＝PN，
∴∠PMN＝∠PNM；
（2）解：
∵点P，M分别是BD，DC的中点，
∴PM∥BC，
∴∠DPM＝∠DBC＝30°
∵点P，N分别是BD，AB的中点，
∴PN∥AD，
∴PN＝AD＝2，∠DPN＝180°﹣∠ADB＝90°，
∴∠MPN＝∠DPM+∠DPN＝120°，
由（1）知，∠PMN＝∠PNM，
∴∠PMN＝∠PNM＝30°，
过点P作PE⊥MN于E，如图：
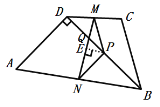
∴∠NPE＝90°﹣∠PNM＝60°，
∴∠EPQ＝∠DPN﹣∠NPE＝30°，
在
中，∴∠PNE＝30°，PN＝2，
∴PE＝PN＝1，
在
中，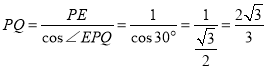
，
故答案为：
．
