题目内容
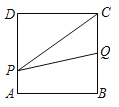
【题目】在![]() 中,
中,![]() ,
,![]() ,以点
,以点![]() 为圆心、
为圆心、![]() 为半径作圆,设点
为半径作圆,设点![]() 为⊙
为⊙![]() 上一点,线段
上一点,线段![]() 绕着点
绕着点![]() 顺时针旋转
顺时针旋转![]() ,得到线段
,得到线段![]() ,连接
,连接![]() 、
、![]() .
.
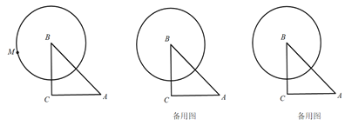
(1)在图中,补全图形,并证明![]() .
.
(2)连接![]() ,若
,若![]() 与⊙
与⊙![]() 相切,则
相切,则![]() 的度数为 .
的度数为 .
(3)连接![]() ,则
,则![]() 的最小值为 ;
的最小值为 ;![]() 的最大值为 .
的最大值为 .
【答案】(1)证明见解析;(2)![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)根据题意,作出图像,然后利用SAS证明![]() ,即可得到结论;
,即可得到结论;
(2)根据题意,由![]() 与⊙
与⊙![]() 相切,得到∠BMN=90°,结合点M的位置,即可求出
相切,得到∠BMN=90°,结合点M的位置,即可求出![]() 的度数;
的度数;
(3)根据题意,当点N恰好落在线段AB上时,BN的值最小;当点N落在BA延长线上时,BN的值最大,分别求出BN的值,即可得到答案.
解:(1)如图,补全图形,
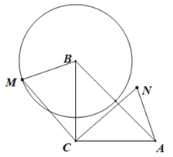
证明:![]()
![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ;
;
(2)根据题意,连接MN,
∵![]() 与⊙
与⊙![]() 相切,
相切,
∴∠BMN=90°,
∵△MNC是等腰直角三角形,
∴∠CMN=45°,
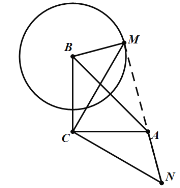
如上图所示,∠BMC=![]() ;
;
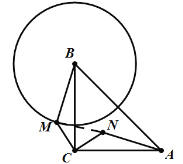
如上图所示,∠BMC=![]() ;
;
综合上述,![]() 的度数为:
的度数为:![]() 或
或![]() ;
;
故答案为:![]() 或
或![]() ;
;
(3)根据题意,当点N恰好落在线段AB上时,BN的值最小;如图所示,
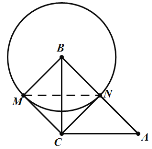
∵AN=BM=1,
∵![]() ,
,
∴![]() ;
;
当点N落在BA延长线上时,BN的值最大,如图所示,
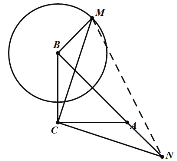
由AN=BN=1,
∴BN=BA+AN=2+1=3;
∴![]() 的最小值为1;
的最小值为1;![]() 的最大值为3;
的最大值为3;
故答案为:1,3.

练习册系列答案
相关题目
【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如下表所示:
的对应值如下表所示:
| ... |
|
|
|
|
| ... |
| ... |
|
|
|
|
| ... |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3![]() 时,
时,![]() 的取值范围.
的取值范围.