题目内容
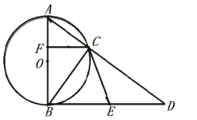
【题目】如图,在△ABC中,∠C=90°,∠A和∠B的平分线交于点P,过点P作PE⊥AB交AB于点E.若BC=5,AC=12,则AE等于______ .
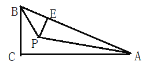
【答案】10
【解析】
过P作PM⊥AC于M,PN⊥BC于N.在直角△ABC中利用勾股定理求出AB的长,由题意可知点P为△ABC内切圆的圆心,设内切圆P的半径为r,利用切线长定理用含r的式子表示出AE=12-r和BE=5-r,根据AB=13列出方程17-2r=13,求出r=2,进而得到AE.
如图,过P作PM⊥AC于M,PN⊥BC于N.
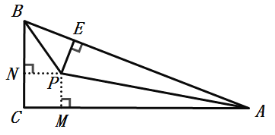
∵在△ABC中,∠C=90°,
∴四边形PMCN为正方形,
∵在△ABC中,∠C=90°,BC=5,AC=12,
∴AB=![]() .
.
∵∠A和∠B的平分线交于点P,
∴点P为△ABC内切圆的圆心,
设直角△ABC内切圆P的半径为r,
∴CM=CN=PM=r,
则AE=AM=AC-r=12-r,BE=BN=BC-r=5-r,
AB=AE+BE=12-r+5-r=17-2r,
∴17-2r=13,
∴r=2,
∴AE=12-2=10.
故答案为:10.

练习册系列答案
相关题目
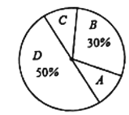
【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.