Question

【题目】在平面直角坐标系xOy中，直线与y轴交于点A,并且经过点B(3，n).

（1）求点B的坐标；

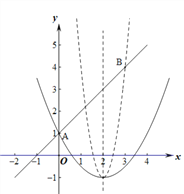
（2）如果抛物线 (a＞0)与线段AB有唯一公共点，求a的取值范围．

Answer 1

【答案】（1）（3，4）；（2）≤a＜

【解析】解：（1）∵直线经过点B(3，n)，

∴把B(3，n)代入解得.

∴点B的坐标为（3，4）.

（2）∵直线y=x+1与y轴交于点A,

∴点A的坐标为（0，1）.

∵抛物线 (a＞0),

∴y = ax2-4ax+4a-1 = a(x-2)2-1.

∴抛物线的顶点坐标为（2，-1）.

∵点A（0，1），点B（3，4）,

如果抛物线y=a(x-2)2-1经过点B（3，4），解得.

如果抛物线y=a(x-2)2-1经过点A（0，1），解得.

综上所述，当≤a＜时，抛物线与线段AB有一个公共点.