题目内容
【题目】在△ABC中,AB⊥BC,AB = BC,E为BC上一点,连接AE,过点C作CF⊥AE,交AE的延长线于点F,连结BF,过点B作BG⊥BF交AE于G.
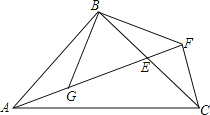
(1)求证:△ABG ≌ △CBF;
(2)若E为BC中点,求证:CF + EF = EG.
【答案】(1)见详解(2)见详解
【解析】
(1)证明∠BAG=∠BCF,∠ABG=∠CBF;即可解决问题.
(2)如图,作辅助线;证明BH=CF,HE=EF;此为解决问题的关键性结论;证明GH=CF,即可解决问题.
解:(1)如图,∵∠ABC=∠AFC=90°,
∴A、B、F、C四点共圆,
∴∠BAG=∠BCF;
∵AB⊥BC,BG⊥BF,
∴∠ABC=∠GBF,
∴∠ABG=∠CBF;
在△ABG与△CBF中,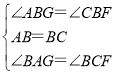 ,
,
∴△ABG≌△CBF(ASA).
(2)
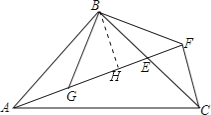
如图,过点B作BH⊥AF;
∵CF⊥AE,
∴BH∥CF,△BHE∽△CFE,
∴BH:CF=GE:EF=BE:CE,
∵BE=CE,
∴BH=CF,HE=EF;
∵△ABG≌△CBF,
∴BG=BF,
∴GH=HF,
∴BH=![]() GF=GH,
GF=GH,
∴GH=CF,而GE=EF,
∴CF+EF=EG.

练习册系列答案
相关题目