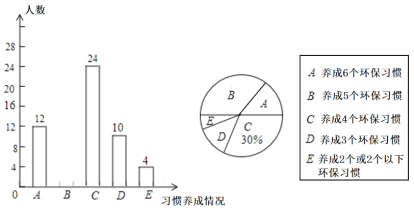
题目内容
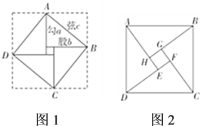
【题目】如图1,在![]() 中,
中,![]() ,
,![]() ,把一块含
,把一块含![]() 角的三角板
角的三角板![]() 的直角顶点
的直角顶点![]() 放在
放在![]() 的中点上(直角三角板的短直角边为
的中点上(直角三角板的短直角边为![]() ,长直角边为
,长直角边为![]() ),点
),点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上.
上.
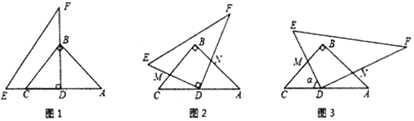
(1)求重叠部分![]() 的面积;
的面积;
(2)如图2,将直角三角板![]() 绕
绕![]() 点按顺时针方向旋转30度,
点按顺时针方向旋转30度,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() .
.
①请说明:![]() ;
;
②在此条件下,![]() 与直角三角板
与直角三角板![]() 重叠部分的面积会发生变化吗?请说明理由,并求出重叠部分的面积.
重叠部分的面积会发生变化吗?请说明理由,并求出重叠部分的面积.
(3)如图3,将直角三角板![]() 绕
绕![]() 点按顺时针方向旋转
点按顺时针方向旋转![]() 度(
度(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)
的结论仍成立吗?重叠部分的面积会变吗?(请直接写出结论,不需要说明理由)
【答案】(1)S△BCD=![]() ;(2)①证明见解析;②重叠部分的面积不变为
;(2)①证明见解析;②重叠部分的面积不变为![]() ;(3)DM=DN的结论仍成立,重叠部分面积不会变.
;(3)DM=DN的结论仍成立,重叠部分面积不会变.
【解析】
(1)重叠部分△BCD是一个等腰直角三角形,求出其直角边,即可求解;
(2)①连接BD,先证得BD=CD,∠C=∠NBD=45°,进而求出△CDM≌△BDN,即可得到DM=DN;②利用①中的结论△CDM≌△BDN即可得出答案;
(3)证明过程类似(2),根据(2)中的结论,可以直接写出.
解:(1)∵AB=BC,AC=2,D是AC的中点,∠ABC=90°,
∴∠BCD=∠A=∠CBD=45°,BD⊥AC.
∴CD=BD=![]() AC=1.
AC=1.
∴S△BCD=![]() CD·BD=
CD·BD=![]() ×1×1=
×1×1=![]() .
.
(2)①连接BD,
∵AB=BC,D是AC的中点,∠ABC=90°,
∴∠C=∠A=∠CBD=∠ABD=45°,
∴BD=CD,∠C=∠NBD=45°,
又∵直角三角板DEF绕D点按顺时针方向旋转30度,
∴∠CDM=∠BDN=30°,
∴△CDM≌△BDN(ASA).
∴DM=DN.
②由①知△CDM≌△BDN,
∴S四边形BNDM=S△BCD=![]() ,
,
即此条件下重叠部分的面积不变为![]() .
.
(3)DM=DN的结论仍成立,重叠部分面积不会变.(证明过程类似(2))