题目内容
【题目】阅读下列材料并完成任务:
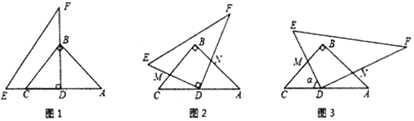
中国古代三国时期吴国的数学家赵爽最早对勾股定理作出理论证明.他创制了一幅“勾股圆方图”(如图l),用数形结合的方法,给出了勾股定理的详细证明.在这幅“勾股圆方图”中,以弦为边长得到的正方形![]() 是由
是由![]() 个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为
个全等的直角三角形再加上中间的那个小正方形组成的.每个直角三角形的面积为![]() ;中间的小正方形边长为
;中间的小正方形边长为![]() ,面积为
,面积为![]() .于是便得到式子:
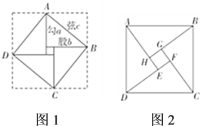
.于是便得到式子:![]() .赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中
.赵爽的这个证明可谓别具匠心,极富创新意识.他用几何图形的截、割、拼、补来证明代数式之间的恒等关系,既具严密性,又具直观性,为中国古代以形证数、形数统一、代数和几何紧密结合、互不可分的独特风格树立了一个典范.如图2,是“赵爽弦图”,其中![]() 、
、![]() 、
、![]() 和
和![]() 是四个全等的直角三角形,四边形
是四个全等的直角三角形,四边形![]() 和
和![]() 都是正方形,根据这个图形的面积关系,可以证明勾股定理.设
都是正方形,根据这个图形的面积关系,可以证明勾股定理.设![]() ,
,![]() ,
,![]() ,取
,取![]() ,
,![]() .
.
任务:
(1)填空:正方形![]() 的面积为______,四个直角三角形的面积和为______;
的面积为______,四个直角三角形的面积和为______;
(2)求![]() 的值.
的值.
【答案】(1)4,96;(2)196.
【解析】
(1)根据题意得图中的四个直角三角形都全等,可得正方形![]() 的边长为2,即可得正方形
的边长为2,即可得正方形![]() 的面积;再利用正方形ABCD的面积-正方形EFGH的面积即可得四个直角三角形的面积和;
的面积;再利用正方形ABCD的面积-正方形EFGH的面积即可得四个直角三角形的面积和;
(2)易求得ab的值,和a2+b2的值,根据完全平方公式即可求得(a+b)2的值,即可解题.
(1)根据题意得,图中的四个直角三角形都全等,
∴AB=c=10,AE-AH=b-a=2,
∴正方形![]() 的面积为22=4,正方形ABCD的面积为102=100,
的面积为22=4,正方形ABCD的面积为102=100,
∴四个直角三角形的面积和=正方形ABCD的面积-正方形EFGH的面积=100-4=96;
(2)由(1)可知四个直角三角形的面积和为![]() ,
,
![]() ,即
,即![]() .
.
![]() ,
,
![]() .
.

【题目】某欢乐谷为回馈广大谷迷,在暑假期间推出学生个人门票优惠价,各票价如下:
票价种类 | (A)学生夜场票 | (B)学生日通票 | (C)节假日通票 |
单价(元) | 80 | 120 | 150 |
某慈善单位欲购买三种类型的票共100张奖励品学兼优的留守学生,其中购买的B种票数是A种票数的3倍还多7张,C种票y张.
(1)直接写出y与x之间的函数关系式;
(2)设购票总费用为w元,求w(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买的学生夜场票不低于20张,且每种票至少购买5张,则有几种购票方案?并指出哪种方案费用最少.