题目内容
【题目】如图,已知矩形ABCD中,AB=2,BC=6,点E从点D出发,沿DA方向以每秒1个单位的速度向点A运动,点F从点B出发,沿射线AB以每秒3个单位的速度运动,当点E运动到点A时,E、F两点停止运动.连接BD,过点E作EH⊥BD,垂足为H,连接EF,交BD于点G,交BC于点M,连接CF. 给出下列结论:①△CDE∽△CBF;②∠DBC=∠EFC;③ ![]() ;④GH的值为定值
;④GH的值为定值![]() ;上述结论中正确的个数为( )
;上述结论中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】试题分析:作CN⊥BD,连接AC.
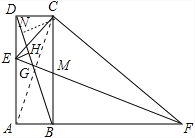
∵四边形ABCD是矩形,AD∥BC,AB=DC,
∴∠CDA=∠DCB=∠DAB=∠ABC=90°,
设E点和F点的运动时间为t,则CE=t,BF=3t,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
在△CDE和△CBF中,
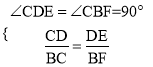 ,
,
∴△CDE∽△CBF,故①正确,
∴∠DCE=∠BCF,
∵∠DCE+∠BCE=90°,
∴∠BCE+∠BCF=90°,
∴∠ECF=90°,
∵![]() ,
,
∴![]() ,
,
∵∠DCB=∠ECF,
∴△DCB∽△ECF,
∴∠DBC=∠EFC,故②正确;
∴∠CDB=∠CEF,
∵∠CDB+∠DCN=90°,∠DCN+∠NCB=90°,
∴∠DCB=∠NCB=∠CEF,
∵CN⊥BD,EH⊥DB,
∴CN∥EH,
∴∠NCE=∠CEH,
∴∠ECB=∠HEG,
∵AD∥BC,
∴∠DEC=∠ECB,
∴∠DEC=∠HEG,
∵∠EDC=∠EHG=90°,
∴△EDC∽△EHG,
∴![]() ,
,
∵AB=DC,
∴![]() ,故③错误;
,故③错误;
∵AD=BC=6,AB=2,
∴BD=![]() =
=![]() ,
,
∵∠EDH=∠ADB,∠EHD=∠DAB,
∴△DEH∽△DBA,
∴![]() ,
,
∴![]() ,
,
∴EH=![]() ,
,
∵![]() ,
,
∴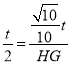 ,
,
∴HG=![]() ,故④正确.
,故④正确.
综上所述①②④正确.
故选C.

练习册系列答案
相关题目