题目内容
【题目】如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.

(1)表中第8行的最后一个数是 ,它是自然数 的平方,第8行共有 个数;
(2)用含n的代数式表示:第n行的第一个数是 ,最后一个数是 ,第n行共有 个数;
(3)求第n行各数之和.
【答案】(1)64,8,15;(2)n2﹣2n+2,n2,2n﹣1;(3)(n2﹣n+1)(2n﹣1).
【解析】试题分析:(1)数为自然数,每行数的个数为1,3,5,…的奇数列,很容易得到所求之数;
(2)知第n行最后一数为n2,则第一个数为n2﹣2n+2,每行数由题意知每行数的个数为1,3,5,…的奇数列,故个数为2n﹣1;
(3)通过以上两步列公式从而解得.
解:(1)每行数的个数为1,3,5,…的奇数列,由题意最后一个数是该行数的平方即得64,
其他也随之解得:8,15;
(2)由(1)知第n行最后一数为n2,且每行个数为(2n﹣1),则第一个数为n2﹣(2n﹣1)+1=n2﹣2n+2,
每行数由题意知每行数的个数为1,3,5,…的奇数列,
故个数为2n﹣1;
(3)第n行各数之和:![]() ×(2n﹣1)=(n2﹣n+1)(2n﹣1).
×(2n﹣1)=(n2﹣n+1)(2n﹣1).

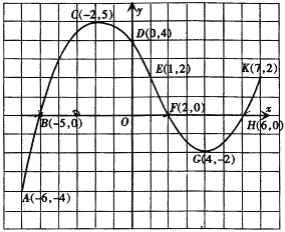
【题目】大家知道,函数图象特征与函数性质之间存在着必然联系.请根据图中的函数图象特征及表中的提示,说出此函数的变化规律.此外,你还能说出此函数的哪些性质?
序号 | 函数图象特征 | 函数变化规律 |
(1) | 曲线从点A(-6,-4)至点K(7,2) | 自变量的取值范围是______. |
(2) | 曲线与y轴交于点D(0,4) | 当x=______时,y=______. |
(3) | 曲线与x轴分别交于点B(-5,0)、F(2,0)、H(6,0) | 当x的值分别为______时,y=0. |
(4) | 曲线经过点E(1,2) | 当x=______时,y=______. |
(5) | 由左至右曲线AC呈上升状态 | 当-6≤x≤-2时,y随x的增大而______. |
(6) | 由左至右曲线CG呈下降状态 | 当______时,y随x的增大而___________. |
(7) | 由左至右曲线GK呈____________ | 当______时y随____________. |
(8) | 曲线上的最高点是C(-2,5) | 当x=______时,y有______值,且这个值为____________. |
(9) | 曲线上的最低点是____________ | 当x=______时,y有______值,且这个值为____________. |
(10) | 曲线BCF位于x轴的上方 | 当______时,y______0. |
【题目】某运动员在一场篮球比赛中的技术统计如表所示:
技术 | 上场时间(分钟) | 出手投篮(次) | 投中 | 罚球得分 | 篮板 | 助攻(次) | 个人总得分 |
数据 | 46 | 66 | 22 | 10 | 11 | 8 | 60 |
注:表中出手投篮次数和投中次数均不包括罚球.
根据以上信息,求本场比赛中该运动员投中2分球和3分球各几个.